img039 (37)

44

<³³⁴»

/(*(a))-/(*(a-+i))

Jeżeli f[x_{k+\)) = O, to x_(t+1) jest jednym z pierwiastków danego równania (3.1) w przedziale (a, b). Jeżeli natomiasty(^x(/t+i)) *■ 0, to sprawdza się, czy spełnione są warunki (3.29) i (3.30). Jeżeli spełnione są warunki (3.29) i (3.30), to współrzędna x_ik\i) otrzymanego punktu przecięcia siecznej z osią Ox jest przyjmowana jako przybliżona wartość jednego z pierwiastków danego równania (3.1) w przedziale (a, b). W przeciwnym razie realizacja algorytmu jest kontynuowana w następnym kroku.

Ciąg (*(*))*= \x ... kolejnych przybliżeń otrzymywany w metodzie reguła falsi może nie być zbieżny. Dlatego też należy podać dopuszczalną liczbę iteracji w celu przerwania obliczeń w przypadku braku zbieżności. Przykład, w którym otrzymuje się ciąg oscylujący, zamieszczono na rys. 3.4.

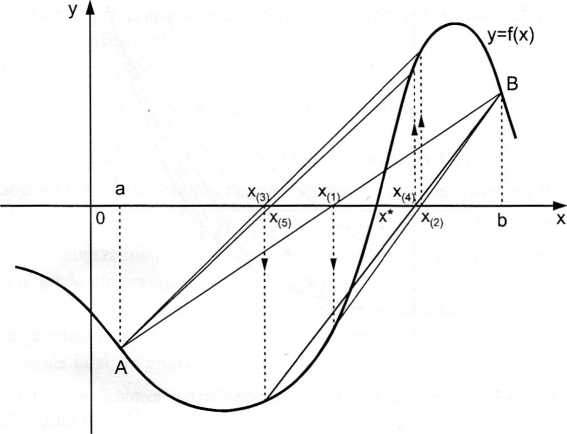
Rys. 3.4. Ciąg kolejnych przybliżeń otrzymany według algorytmu reguła falsi tworzy tu ciąg oscylujący

Ma miejsce następujące twierdzenie dotyczące zbieżności ciągów kolejnych przybliżeń otrzymywanych w metodzie reguła falsi.

Twierdzenie 3.1 [8]

Jeżeli funkcja ciągła j{-) występująca w danym równaniu (3.1) spełnia warunek (3.3), jest klasy C² w zadanym przedziale {a, b) oraz pochodne/'(•) i/"(0 mają w przedziale {a, b) stały znak, to:

— w przedziale (a, b) znajduje się dokładnie jeden pierwiastek równania (3.1);