img473 (3)

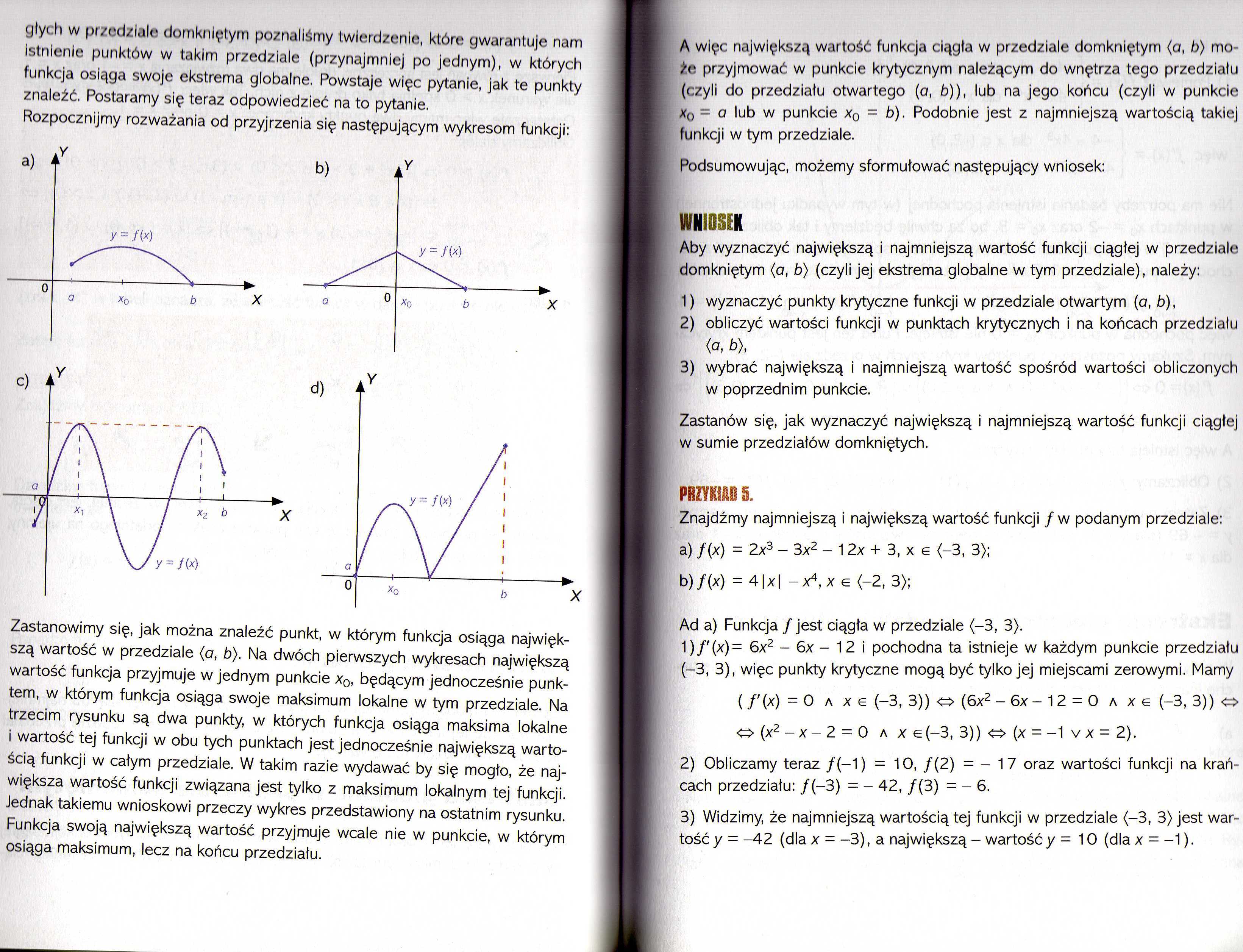
(jlyc h w przedziale domkniętym poznaliśmy twierdzenie, które gwarantuje nam Istnienie punktów w takim przedziale (przynajmniej po jednym), w których funkcja osiąga swoje ekstrema globalne. Powstaje więc pytanie, jak te punkty znaleźć. Postaramy się teraz odpowiedzieć na to pytanie.

Rozpocznijmy rozważania od przyjrzenia się następującym wykresom funkcji:

Zastanowimy się, jak można znaleźć punkt, w którym funkcja osiąga największą wartość w przedziale (a, b). Na dwóch pierwszych wykresach największą wartość funkcja przyjmuje w jednym punkcie x₀, będącym jednocześnie punktem, w którym funkcja osiąga swoje maksimum lokalne w tym przedziale. Na trzecim rysunku są dwa punkty, w których funkcja osiąga maksima lokalne i wartość tej funkcji w obu tych punktach jest jednocześnie największą wartością funkcji w całym przedziale. W takim razie wydawać by się mogło, że największa wartość funkcji związana jest tylko z maksimum lokalnym tej funkcji. Jednak takiemu wnioskowi przeczy wykres przedstawiony na ostatnim rysunku. Funkcja swoją największą wartość przyjmuje wcale nie w punkcie, w którym osiąga maksimum, lecz na końcu przedziału.

A więc największą wartość funkcja ciągła w przedziale domkniętym (a, b) może przyjmować w punkcie krytycznym należącym do wnętrza tego przedziału (czyli do przedziału otwartego (a, b)), lub na jego końcu (czyli w punkcie x₀ = a lub w punkcie x₀ = b). Podobnie jest z najmniejszą wartością takiej funkcji w tym przedziale.

Podsumowując, możemy sformułować następujący wniosek:

WNIOSEK

Aby wyznaczyć największą i najmniejszą wartość funkcji ciągłej w przedziale domkniętym (a, b) (czyli jej ekstrema globalne w tym przedziale), należy:

1)    wyznaczyć punkty krytyczne funkcji w przedziale otwartym (a, b),

2)    obliczyć wartości funkcji w punktach krytycznych i na końcach przedziału (a, b),

3)    wybrać największą i najmniejszą wartość spośród wartości obliczonych w poprzednim punkcie.

Zastanów się, jak wyznaczyć największą i najmniejszą wartość funkcji ciągłej w sumie przedziałów domkniętych.

PRZY11AD S.

Znajdźmy najmniejszą i największą wartość funkcji / w podanym przedziale:

a)    f{x) = 2x³ - 3x² - 1 2x + 3, x e (-3, 3);

b)    /(x) = 4|x| -X⁴, x e (-2, 3);

Ad a) Funkcja / jest ciągła w przedziale (-3, 3).

1 )y'(x)= 6x² - 6x - 1 2 i pochodna ta istnieje w każdym punkcie przedziału (-3, 3), więc punkty krytyczne mogą być tylko jej miejscami zerowymi. Mamy

( f (x) = O a x g (-3, 3)) o (6x² - 6x - 1 2 = O a xg (-3, 3)) o

<=>(x²-x-2 = 0 a x g(-3, 3))o(x = -1vx = 2).

2) Obliczamy teraz /(—1) = 10, /(2) = - 17 oraz wartości funkcji na krańcach przedziału: /(—3) = - 42, /(3) = - 6.

3)    Widzimy, że najmniejszą wartością tej funkcji w przedziale (-3, 3) jest wartość y = -42 (dla x = -3), a największą - wartość y = 10 (dla x = -1).