MF dodatekA04

Dodatek A.2 Funkcja liniowa, wykładnicza i logarytmiczna 249

Szereg liczbowy, którego wyraz ogólny a_n jest n tym wyrazem ciągu geometrycznego

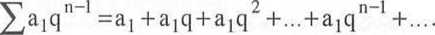
A(1.16)

n=i

nazywamy szeregiem geometrycznym.

Jeżeli lql<1, to szereg geometryczny jest zbieżny i ma sumę równą:

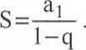
A(1 -17)

W przeciwnym przypadku (gdy lql>1) szereg geometryczny jest rozbieżny. A2. Funkcja liniowa, wykładnicza i logarytmiczna

Funkcja f odwzorowująca zbiór X na zbiór Y jest to przyporządkowanie każdemu elementowi xeX dokładnie jednego elementu ye Y.

Funkcją f: Xh>Y zapisujemy x-» y=f(x), gdzie xeX, yeY przy czym

x - nazywamy argumentem funkcji lub zmienną niezależną, y - nazywamy wartością funkcji f lub zmienną zależną, f - jest symbolem funkcji (odwzorowania),

X - nazywamy dziedziną lub zbiorem argumentów funkcji.

Wykresem funkcji y=f(x) nazywamy zbiór punktów (x, f(x)), gdzie x należy do dziedziny funkcji.

Funkcję f nazywamy rosnącą w zbiorze X, gdy dla każdych dwóch liczb X-, i x₂ z tego zbioru

A(2.1)

x₁ < x₂ => f(x₁ )<f(x₂)