image031 (19)

B. \^rirm>rtko.    sztcine. Waisowi 2007.

ISaN!978-Si-«<SCC.U.8.« by WAlP 200?

toksttHsłępedagogwnP 63

Droga pana Technologowicza do pracy w szkole była odmienna i jego start zawodowy wypadł inaczej.

Mundka interesował traktor i chętnie zostałby na wsi, ale jego ojciec uznał, ze najmłodszy i najzdolniejszy w rodzinie powinien być wysłany do liceum ogólnokształcącego. Gdy usłyszał, ze syn chciałby studiować matematykę, powiedział „No więc tak! Zostaniesz nauczycielem", na co chłopiec gwałtownie zaprzeczył, bo praca w szkole wydawała mu się nudna. Na wszelki wypadek zapisał się jednak na uczelniany kurs pedagogiczny. Na tym kursie przeprowadził swoją pierwszą lekcję.

(1)    „Dam panu świetny temat - powiedział starszy nauczyciel o wyglądzie człowieka nieporadnego - dzielenie ułamka przez ułamek". Edmund przygotował się starannie z kilku podręczników, skserował parę ćwiczeń z przykładami, grafami, osią liczbową i prostokątami, napisał długi konspekt lekcji problemowej, ale już po paru minutach wiedział, że najlepsi uczniowie nie pozwolą mu go zrealizować, bo znają temat z podręcznika, a przywykli rządzić lekcją matematyki, „świetnie!"-powiedział student - „rozwiążecie te oto zadania na szóstkę, a potem opowiecie, jak rozumowaliście". Sam zajął się słabszymi uczniami, którzy, jak się okazało, mieli kłopot z dzieleniem ułamków przez liczbę całkowitą, a nawet z pojęciem ułamka jako stosunku dwu liczb. W drugiej części lekcji matematyczne orły przedstawiły swoje pomysły interpretacji dzielenia ułamków jako odwrotności mnożenia. Zrobiło się interesująco, a Edmund, po przejrzeniu rozwiązań, postawił dwie szóstki i trzy piątki.

„Kiedy pan znów przyjdzie do nas?" - odprowadzając go na korytarz, pytali, nie tylko najlepsi uczniowie. Największe uznanie spotkało go jednak dopiero w pokoju nauczycielskim. „Pan jest nie tylko nauczycielem - powiedział stary matematyk, który przysłuchiwał się pilnie lekcji debiutanta w swojej klasie - pan jest pedagogiem!’

Potem pochłonęła Edmunda algebra i został asystentem w Katedrze Funkcji Rzeczywistych na uniwersytecie. Zajęcia ze studentami nie dawały mu jednak satysfakcji, a wręcz przeciwnie - złościły, ze względu na ich elementarne braki ze szkoły średniej, a nawet podstawowej. „Jak was uczono matematyki?"

- wzdychał, gdy kolejni pechowcy żegnali się z uczelnią. Po dwóch latach poprosił swego szefa o rozmowę, która przebiegła następująco:

(2)    Technologowicz: Panie profesorze! Postanowiłem podjąć pracę w gimnazjum. Profesor: Jak to? A doktorat?

T: Mam temat z dydaktyki. Muszę zdobyć doświadczenie.

P: Przecież prowadzi pan zajęcia...

T: Ale nieskutecznie. Moi studenci byli tak nauczani, że w żaden sposób nie mogę pobudzić ich myślenia. Matematycznego! A co dopiero mówić o twórczości dydaktycznej.

wv/w.waip.com.pl

B, Nirmmko. Kctafame akotne. Wmzaw* 2007. ISaN V7S-83-OOSCC-l 1-B. < ły, WAlP 2007

64 Rozdział 2. Poznajmy się Ncei uczniów I nauczyciele

P: Więc będzie pan budował metodykę elementarną?

T: Spróbuję. A gdy mi się uda, to wrócę na uczelnię.

P: No, no... Życzę powodzenia!

Już podczas swej pierwszej lekcji próbnej pan Technologowicz wykazał się cenną umiejętnością działania modyfikacyjnego. to jest natychmiastowego korygowania planu według napotkanych warunków, skuteczniejszego od działania schematycznego, dokonywanego ściśle według planu, a przeważającego u nowicjuszy {Maciaszek, 1965, s. 73). Modyfikacje zajęć na uczelni nie wystarczały jednak, by usunąć błędy metodyczne popełniane na niższych szczeblach kształcenia. To skłoniło pana Technologowicza do podjęcia pracy nauczycielskiej u podstaw.

System kształcenia i sytuacja dydaktyczna

Już po kilku latach pracy w szkole pani Felicja rozwinęła swój warsztat pedagogiczny w humanistyczny system kształcenia. Aby go dobrze objaśnić, musimy umówić się co do znaczenia pojęcia system kształcenia. Będziemy tak nazywać celowy układ sytuacji dydaktycznych, to jest układ, w którym każda sytuacja jest etapem osiągania określonych celów kształcenia, rozumianych jako zamierzone właściwości uczniów. Można to sobie wyobrazić w następujący sposób:

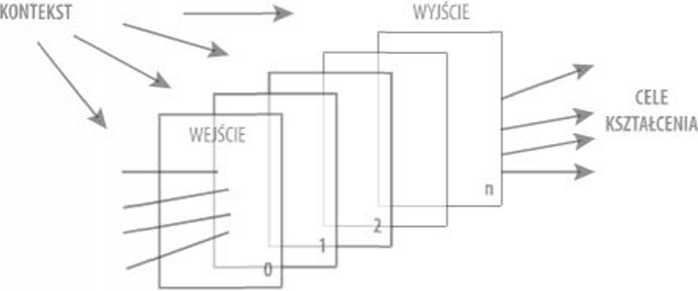
Rysunek 4. System kształcenia jako układ sytuacji dydaktycznych \^Ta rysunku 4 widzimy:

1. cele kształcenia - w postaci pęku strzałek wskazujących wybrane kie runki działania edukacyjnego,