image161 (7)

B. Nirm*iko. KattUcente aioine. Wanrawi 2007. ISBN 978-K3-ĆCI&CI?■1I-8,< by WAlP 2007

Skale rtonwow 321

Ocena pozycyjna ma znikome znaczenie treściowe, bo jedynie ogólnie określa dziedzinę osiągnięć ucznia, a nie mówi, jakie czynności opanował, a jakich nie opanował. Jej zaletą jest to, że może być przedstawiona w skali przedziałowej, co znaczy, że konstrukcję odpowiedniej skali zaczynamy od zdefiniowania jednostki pomiaru.

Jednostką pomiaru różnicującego c/.yn imy całość lub część odchylenia standardowego wyników pomiaru, będącego miarą rozrzutu tych wyników, a skale oparte na odchyleniu standardowym wyników nazywamy skalami standardowymi. Sposób obliczania odchylenia standardowego podają podręczniki statystyki i statystyczne programy komputerowe.

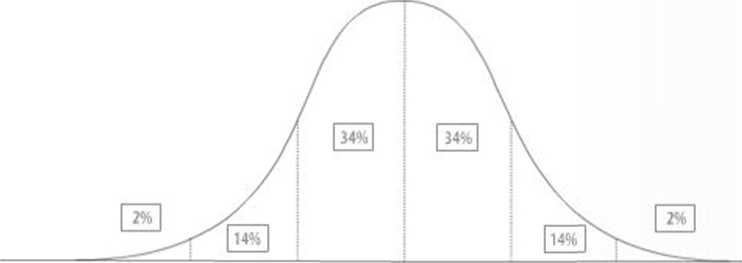
Najbardziej użyteczne są standardowe skale znormalizowane, w których częstość poszczególnych ocen pozycyjnych jest wyznaczona teoretycznym rozkładem normalnym (Gaussa), opisanym krzywą o charakterystycznym kształcie dzwonowym (rys. 17). Pod rysunkiem pokazano trzy znormalizowane skale standardowe, będące w użyciu w egzaminach zewnętrznych w Polsce.

Odchylenie standardów L

Skala standardowej	1	2 1	I	3	|	4	5 I
piątki	7%	24%		38%		24%	7%
Skala stamnowa (standardowi	1 _L	2 3 1 1	4 _L	5 _L	6 _J	7	8 I	9
dziewiątki)	4%	7% 12%	17%	20%	17%	12%	7%	4%
Skala akademicka 20(J (CEEB. 200 - 800) |	300 1	400 1		500 |		600 |	700 I	800 _J
	2%	14%	34%		34%		14%	2%

Rysunek 17. Rozkład normalny i trzy standardowe skale znormalizowane

wv/w.waip.com.pl

B. Nirmyrrku, KiZOtfanie siebie, Wbrszawa 2007. ISBN >*78^3^0507.11 -8. t by WAlP 2007

322 Rozdział io. Nauczy oH ocena ost^męda uamów

Skala standardowej piątki ma średnią arytmetyczną równą 3 punkty (taki wynik uzyskuje aż 38% egzaminowanych), a odchylenie standardowe równe 1 punkt. Tak krótka skala jest stosowana w komisjach egzaminacyjnych do pokazania rozkładu osiągnięć uczniów w testkach, czyli wyodrębnionych treściowo częściach testu (arkusza egzaminacyjnego).

Skala staninowa ma średnią arytmetyczną równą 5 punktów, a odchylenie standardowe równe 2 punkty. Taka skala jest stosowana do przedstawiania ogólnych wyników poszczególnych uczniów i średnich wyników szkół. Mówimy: „uczeń uzyskał pięć Staninów'” albo „uzyskał o dwa Staniny więcej od średniej swojej szkoły". Kolejne Staniny mają nazwy: 1 - najniższy, 2 - bardzo niski, 3 - niski, 4 - niżej średni, 5 - średni, 6 - wyżej średni, 7 - wysoki, 8 - bardzo wysoki, 9 - najwyższy.

Najmniej jeszcze popularna w Polsce jest skala akademicka - o średniej 500 punktów^ i odchyleniu standardowym 100 punktów'. Jest stosowana (zwykle pełnymi dziesiątkami punktów) w' testach w-stępnych na wyższe uczelnie w^r Stanach Zjednoczonych, a także w międzynarodowych badaniach osiągnięć uczniów (OF.CD). Planuje się zastosow-anie jej, jako pomocniczej, do egzaminu maturalnego.

Przekształcanie dowolnego rozkładu wyników' pomiaru na rozkład normalny jest dość złożoną procedurą, opisaną w' podręcznikach pomiaru (Niemierko, 1975, s. 147-150; Niemierko, 1999, s. 267-274), a usprawnianą przez technikę komputerowy. Pozycja osiągnięć ucznia w^r zbiorze wyników egzaminu może być przedstawiona z dużą precyzją, ale - przypomnijmy - żadna miara pozycyjna osiągnięć ucznia nie mówi nam o tym, czy określone wymagania programowa są przez niego spełnione.

Pseudonormy wymagań

Matematyczny urok skal znormalizowanych powoduje, że nie ustają próby wykorzystania pewmych cech rozkładu wyników pomiaru dydaktycznego do „naukowego” definiowania wymagań i oceniania osiągnięć uczniów. Tc próby są daremne, ponieważ to, co jest, nie mówi nam o tym, co powinno być - żaden empiryczny rozkład osiągnięć uczniów nie może nam dyktow^rać osiągnięć zamierzonych w' programach i planach dydaktycznych. Zatem, nie da się zamienić różnicowania na sprawdzanie, choć odwrotna operacja jest możliw^ra, bo spraw'-dzanie przynosi zwykle pewien rozrzut wyników (Popham i Husek, 1969).

Pseudonormami wy magań naz wiemy normy osiągnięć uczniów oparte na założeniach statystycznych, a pozbawione uzasadnienia programowego. Takie normy zacierają granicę między różnicowaniem a sprawdzaniem. Mogą być użyteczne jako informacja pomocnicza, na tej samej zasadzie, jak wyniki badań próbnych