Image48 (12)

94

L =

i m x² (1 + tg²a)

mgx tga =

m

!2

2 cos²a

mgx tga

Stąd

dL

dx

= -mg tga,

d /d£

m

dt \dx

cos²a

Podstawiając te wyrażenia do równania Lagrange’a mamy

x + ^ g sin2a

= 0

Całkując to równanie i uwzględniając warunki początkowe otrzymujemy

x =

^ gt² sin2a 4- H ctga

Czas ruchu znajdujemy z warunku x(t_k) = 0, czyli

U =

1

sina

2II

G

n

Czas ruchu jest najmniejszy przy cl — -

JL

2.35. Obierając zmienną r jako współrzędną uogólnioną i uwzględniając, że

<P =

otrzymujemy funkcję Lagrange’a

L = m (r² — co¹ r²),

2 _2

gdzie

k

co

m

Stąd równanie Lagrange’a przybiera postać

r + co² r = 0.

Jest to równanie oscylatora harmonicznego nietłu niem jest funkcja

II

ionego. Jego rozwiąza-

r = A cos (a)t -j- P),

która ma jednak sens jedynie dla r ^ 0.

Gdyby cząstka po dojściu do punktu r = 0 uległa sprężystemu odbiciu, wówczas

r =

A cos (ot 4- P)\,

2.36. Układ przedstawiony na rys.29 ma dwa stopnie swobody. Jako współrzędne uogólnione obieramy kąty a_A i a₂. Energie kinetyczną i potencjalną układu wyrażamy przez wybrane współrzędne uogólnione.

Dla	mv:
	1
Ekl	= -mlV
	II
Dla	m2:

2 _

1

2

,2 _

1

2

2 J2

czyli

	sina!	+	W	sina2,
^li a1	cosa!	+	h	• a2 cosa2,
= /,	cosaj	+	^2	cosa2,
-(/, oi	! sina!	+	k	a2 sina2),

m.

~2

—

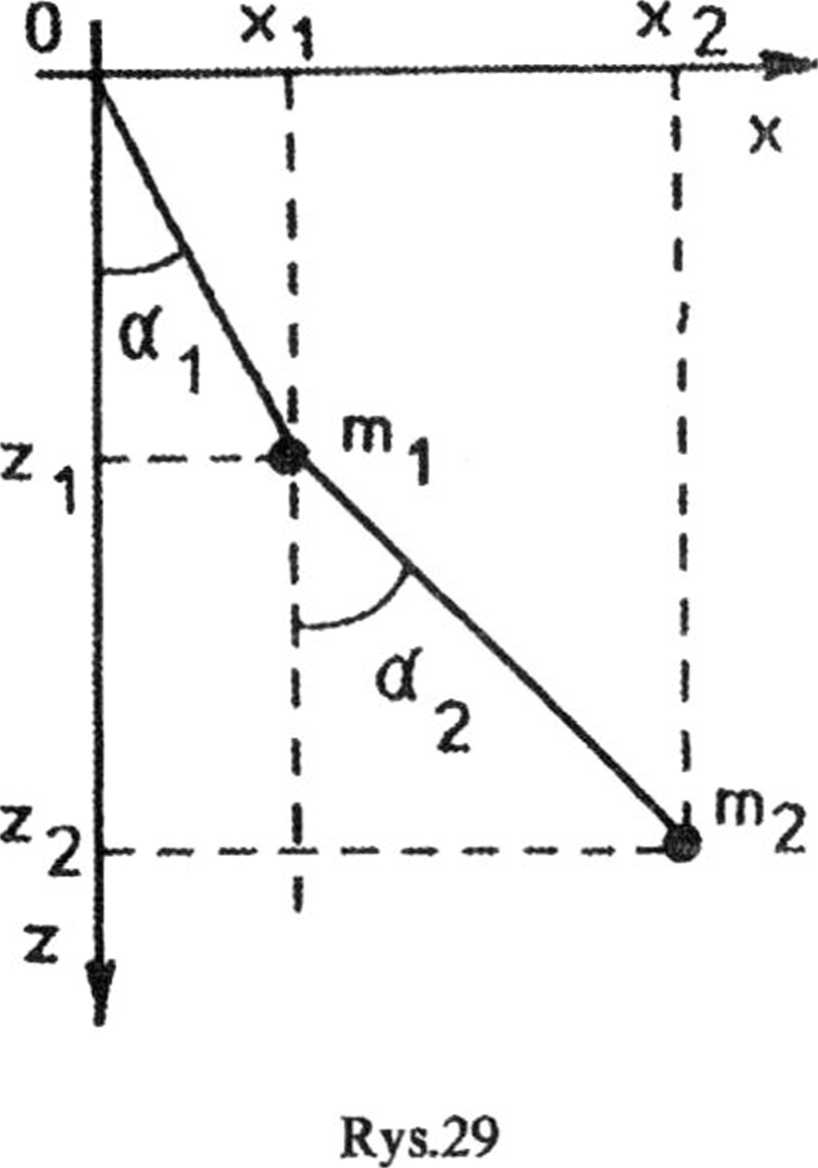
m

k2

2

(l² a² -f 2/₁ l₂ ol₁ cc₂ cos(a₁ —

a₂) + Ił aj),

E _p2 = ~m₂gz₂

m₂g (l_L cosa₁ + l₂ cosa₂).