s70 71

70

L3. Funkcję podcałkową rozkładamy na ułamki proste:

70

x — 5

7x + 2

(x — 5)(x^{1 2} +12)

A Bx + C

⁺ X² + 12 ’

a więc po pomnożeniu przez (x — 5)(x² + 12) mamy

7x + 2 = A(x² + 12) + (Bx + C)(x — 5). Porównajmy współczynniki przy równych potęgach x :

x

x

x

0 — A +

7 = -5 B + C, 2 = 12,4 - 5C.

Rozwiązaniem tego układu są wartości liczbowe:

A = 1,    B=-l, C — 2,

a więc

(x — 5)(x² + 12)

7x + 2

dx

1

x — 5

c/x +

—x + 2 x² + 12

dx

Oczywiście

dx

5

ln |x — 5| 4- C\.

Obliczmy teraz drugą z tych całek, mianowicie

—x + 2 X² + 12

dx

x

x² + 12

dx + 2

dx

x² + 12

1

2

1

2

2x

x² + 12

dx +

dx

12

2x ,    1

—--dx H—

x² + 12    6

1 + — ' 12

dx

1 +

(+)

2

Podstawmy

x² + 12

u

2xdx — du.

x

\/l2

t

dx

2v/3

dt,

odpowiednio dla pierwszej i drugiej całki. Stosując teraz twierdzenie o całkow niu przez podstawienie, mamy

^r‘ -x + 2 x² + 12

<lx = -i

' du 2 \/3 2 1    u6

dt

1 + t²

-ln

2

u

v/3

+ — arct.g + C_>

O

Stąd wynika końcowa odpowiedź:

(X ~h 2

(x — 5)(:r² -f 12)

dx — ln

x — 5| — ^ ln(:i*² 4- 12) +

Z    ó

X

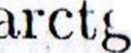
r

2v/3

+

14. Podstawmy

\/x’ — t,

a stąd

x — t⁶

oraz

c/x = 6t^r*dt.

Wówczas

dx = 6

'* t⁶ -f t⁴ + t ,₅

£⁶(1 + £²)

,,    * f⁶(*⁵ + i³ +1),

t dt — 6 / -—--—-dt

₆ f±il±^

<² +1

i? + 1

r	\ li			-1 w* fv MM _i
*j	ł^3 4- ^+ ! 4- t^2 _	a- ii	= 6	— + arctg t

Q _

+ C

~ n/Jt² + 6arctg\/x ?

i?(sin x, cos :/;)dx,

gdzie i?.(sin a:, cos.x) oznacza funkcję wymierną względem sinx i cos:/:. W taki

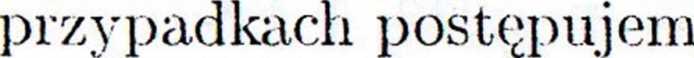
,y następująco:

(i) Jeżeli

R(— sina:, cos:/;) = — R(sinx, cos:/;),

tzn. gdy funkcja U jest nieparzysta względem sin:/:, to stosujemy podstaw nie

1

   , .    \/3    x- ^

2

   + ¹²) + — arct,g^= + C₂.