img154

1

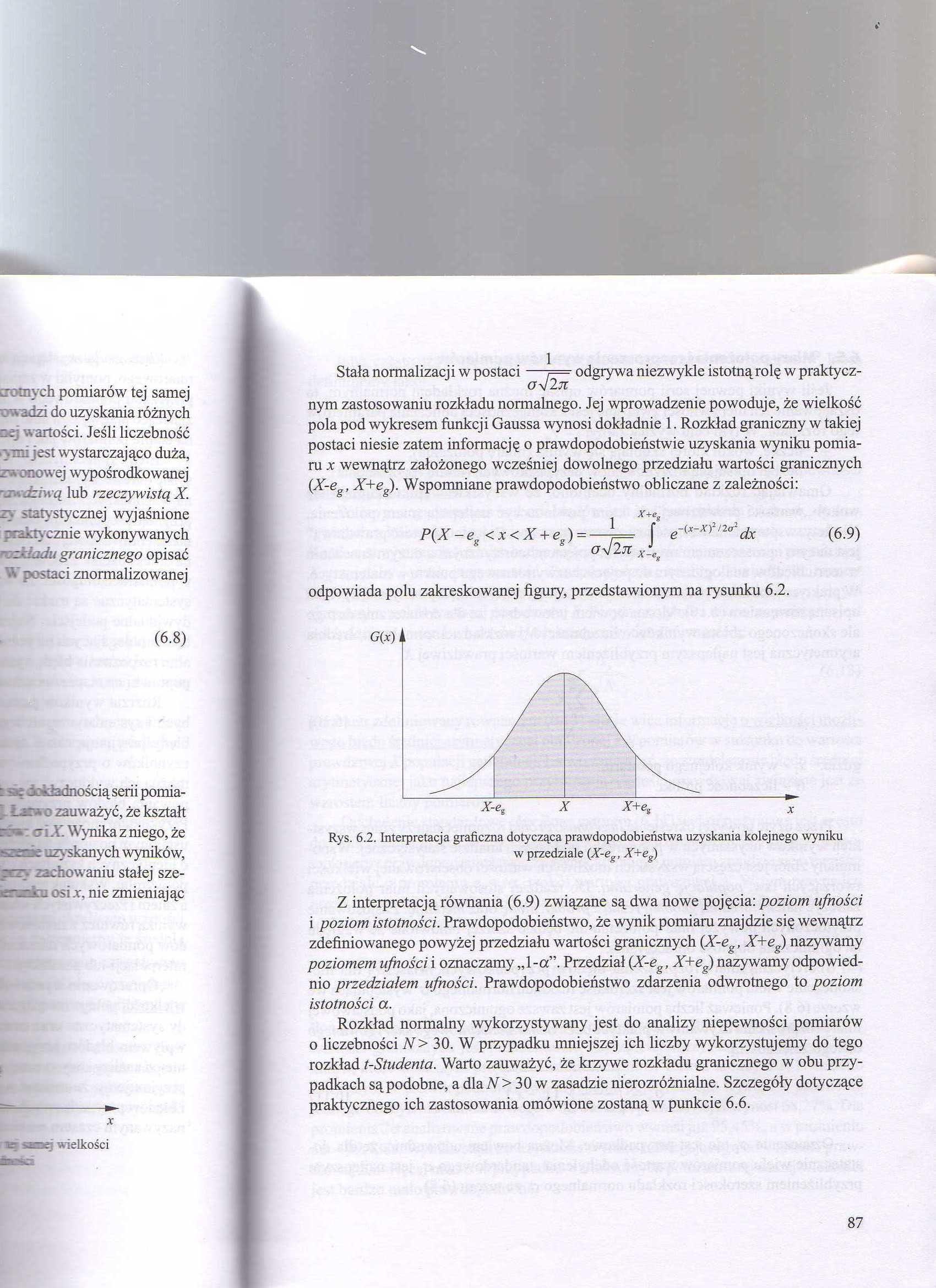
Stała normalizacji w postaci —j= odgrywa niezwykle istotną rolę w praktycz-

ofljl

nym zastosowaniu rozkładu normalnego. Jej wprowadzenie powoduje, że wielkość pola pod wykresem funkcji Gaussa wynosi dokładnie 1. Rozkład graniczny w takiej postaci niesie zatem informację o prawdopodobieństwie uzyskania wyniku pomiaru x wewnątrz założonego wcześniej dowolnego przedziału wartości granicznych (X-e , X+e_g). Wspomniane prawdopodobieństwo obliczane z zależności:

X+e„

P(X-e<x<X + e) =

-(x-X)²/ 2a^l

O

\fljt _x__e

dx

(6.9)

odpowiada polu zakreskowanej figury, przedstawionym na rysunku 6.2.

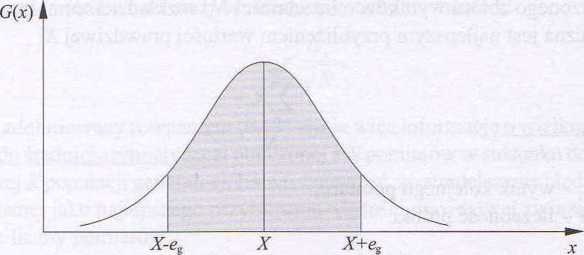
Rys. 6.2. Interpretacja graficzna dotycząca prawdopodobieństwa uzyskania kolejnego wyniku

w przedziale (X-e_g, X+e_?)

Z interpretacją równania (6.9) związane są dwa nowe pojęcia: poziom ufności i poziom istotności. Prawdopodobieństwo, że wynik pomiaru znajdzie się wewnątrz zdefiniowanego powyżej przedziału wartości granicznych (X-e_g, X+e_g) nazywamy poziomem ufności i oznaczamy „1-a”. Przedział (X-e_g, X+e_g) nazywamy odpowiednio przedziałem ufności. Prawdopodobieństwo zdarzenia odwrotnego to poziom istotności a.

Rozkład normalny wykorzystywany jest do analizy niepewności pomiarów o liczebności N> 30. W przypadku mniejszej ich liczby wykorzystujemy do tego rozkład t-Studenta. Warto zauważyć, że krzywe rozkładu granicznego w obu przypadkach są podobne, a dlań/" > 30 w zasadzie nierozróżnialne. Szczegóły dotyczące praktycznego ich zastosowania omówione zostaną w punkcie 6.6.