img258

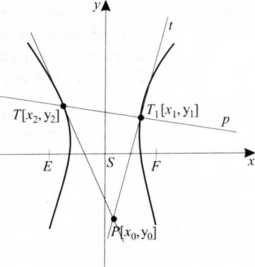
Styczna i zmienne biegunowe hiperboli

Styczna hiperboli w punkcie T\x.\y.]: xx. yy

5[0;0], EFc.x\ —--— = \,

S[m;n], EF\\x:

(■x-m)(x_i-m)    (y~n)(y_t-n)

a²    b²

Zmienne biegunowe hiperboli i należące do bieguna /^>[x₀;.V₀]:

^xxc\ yy_n

S[0;0], EF ci:    = |.

a² b²

or n _rc., (x-m)(x₀-m)    (y-n)(y₀-n)

S[m\n). EF\\x: -------= 1

a¹    b₂

Analogicznie dla innych pozycji biegunowych.

Równanie asymptot

Równanie asymptot hiperboli:

S[0;0], EFcx: y = -x, y=--x, a    a

S[m\n], EF\\x: y = ~(x-m)+/t, y= -—(x-m)+n. a    a

Analogicznie dla innych pozycji stożkowych.

Równanie hiperboli rów noosiow ej z asymptotami w osiach układu w spółrzędnych albo równoległy mi do osi układu współrzędnych

I li perbol a rów noosiow a:

S[0; 0], główna oś wyrażona w prostej k = 1:

S[m; n\, główna oś wyrażona w prostej k = -1: S[0;0], główna oś wyrażona w prostej k = 1: S[w; n], główna oś wyrażona w prostej k = -1:

yk

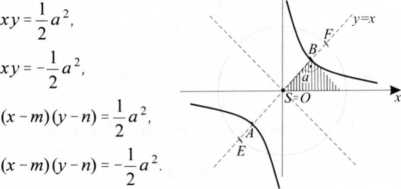
Równania stożkowych w pozycji środkowej (okrąg, elipsa, hiperbola)

Wszystkie równania środkowych pozycji stożkowych można przekształcić w postać: ±p²(x -m)²±q²(y -ri)² = ±s².

Rów nanie stycznej do środkowej pozycji stożkowej w punkcie 7’[je_|;_iy_|]: ±p²(x-m)(x_l -m)±q²(y-n)(y_] -n)=±s².

44