img279 (6)

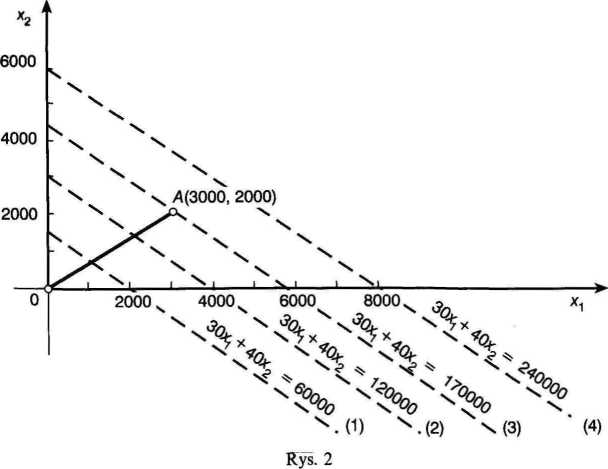
Kierunek przesuwania izolinii wynika z kryterium optymalizacji (funkcji celu). W rozważanym przykładzie funkcja celu F jest maksymalizowana. Oznacza to, że kolejno przyjmujemy coraz to większe wartości wyrazu wolnego przesuwanej prostej [patrz rys. 2, izolinie (1) —(4], Izolinie (1) i (2) przecinają odcinek O A i dopiero izolinia (3) trafia na jego koniec w punkcie A. Izolinia (4) została zaś zbyt daleko przesunięta i znalazła się poza odcinkiem rozwiązań dopuszczalnych. Proste (1) —(4) tworzą rodzinę izolinii, tj. linii, w których parametry przy zmiennych pozostają bez zmian, a zmieniają się jedynie wartości wyrazów wolnych. W zależności od sytuacji {F -* max bądź F -> min) wartości wyrazu wolnego należy zwiększać lub zmniejszać. Punktem najdalej wysuniętym na odcinku O A w sensie równoległego przesunięcia jest zatem punkt A. Współrzędne tego punktu = 3000 oraz X2 = 2000 są optymalnym rozwiązaniem zadania. Wartość przychodu ze sprzedaży przy uwzględnieniu optymalnego asortymentu wyniesie więc F(x*₁,X2)= 170 000 zł.

Przykład 2. Przedsiębiorstwo produkuje dwa wyroby: W₁ i W₂. Dwa z wielu środków produkcji są limitowane. Limity te wynoszą: środek 1-36 000 jedn., środek II - 50 000 jedn. Nakłady limitowanych środków na jednostkę produkcji podano w tabl. 2.

Tablica 2

Środki	Jednostkowe nakłady
produkcji	W[	W2
I	6	6
II	10	5

Należy także uwzględnić, że zdolność produkcyjna jednego z agregatów nie pozwala wyprodukować więcej niż 4000 szt. wyrobu W₂. Nie ma natomiast żadnych dodatkowych ustaleń w stosunku do wyrobu W_x.

Określić optymalne rozmiary produkcji, przy założeniu że zysk realizowany na obu wyrobach jest jednakowy. Przy rozwiązywaniu zastosować metodę geometryczną.

Rozwiązanie. Przystępując do budowy modelu, przyjmujemy oznaczenia:    - wielkość produkcji wyrobów W_1; x₂ - wielkość produkcji

wyrobów W₂. Pierwsze dwa warunki ograniczające dotyczą limitów na środki

produkcji I i II:
O)	ójCj + 6x2 36000,
(2)	10xt + 5x2< 50000.
Warunek brzegowy dla zmiennej x1 ma postać:
(3)	x1 ^0.
Warunek brzegowy dla zmiennej x2 ze względu na ograniczenie od góry ma postać:
(4)	0^x2s£4000.
Jak się łatwo domyślić, gdy mowa o optymalnym rozwiązaniu, kryterium optymalności tego zadania stanowi wielkość łącznego zysku osiągnięta ze sprzedaży wyrobów Wj i W2. Ponieważ zysk jednostkowy na obu wyrobach jest jednakowy, przeto i parametry w funkcji celu powinny być jednakowe, a najprościej można przyjąć, że są równe jedności. Funkcja celu jest zatem następująca:
(5)	F(x1,x2) = Xj +x2-> max,
a cały model ma postać:
(1)	6xt + 6x2< 36000,
(2)	10xj + 5x2< 50000,
(3)	X1ćt0.
(4)	0^x2< 4000,
(5)	F(xv x2) — xt + x2 -* max.

Ze względu na warunki (3) i (4) rozwiązanie zadania, jeżeli rozwiązanie to istnieje, musi się znaleźć w pierwszej ćwiartce układu współrzędnych. Podobnie jak w przykładzie 1, poszczególne relacje ponumerowano (rys. 3).

Pole zakreskowane na rys. 3 stanowi obszar rozwiązań dopuszczalnych, gdzie należy szukać rozwiązania optymalnego. Przesuwając równolegle izo-linię CD stwierdzamy, iż jej najdalsze możliwe przesunięcie pokryje się z odcin-