img099

8.1. Postawienie zadania i podstawowe założenia

99

Q

optymalna funkcja przynależności

C

Rys. 8.1. Wartość funkcji kryterialnej Q zależy od wybranej postaci funkcji przy-

należności C. Zwykle zależność ta ma minimum, którego osiągnięcie można utoż-

samiać z wyborem optymalnej techniki rozpoznawania

Na podstawie przyjętych założeń, charakteryzujących zadanie klasyfikacji A (por. (14)), można budować ocenę jakości Q(A,A) algorytmu rozpoznającego A_} a następnie można poszukiwać takiej formy funkcji przynależności C^l(x), aby minimalizować Q(A,A) (rys. 8.1).

Budowę oceny Q(i4,^4) przeprowadzimy etapowo. Najpierw zdefiniujemy oczekiwaną wartość oceny (straty) dla pewnego ustalonego obiektu x przy przyjęciu pewnej, ustalonej decyzji t. Oznaczając tę stratę przez Q^l(x)₎ możemy zapisać

L

(86)

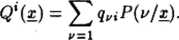
Prawdopodobieństwo p(v/x) określające, że mamy do czynienia z obiektem klasy v € /, jeśli zaobserwowano wektor cech x£X_} obliczyć można na podstawie przytoczonych danych, opierając się na wzorze Bayesa:

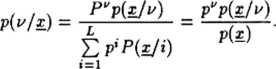
(87)

Na podstawie znajomości strat warunkowych Q*(x) oraz apriorycznych prawdopodobieństw klas p* obliczyć można uogólnioną stratę Q(x;) ocze-