img280 (6)

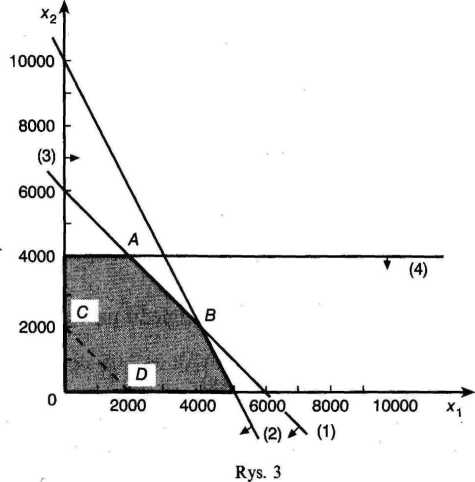
kiem AB. W tym przypadku mamy nieskończenie wiele rozwiązań (rozwiązania te stanowią współrzędne wszystkich punktów odcinka AB). W szczególności rozwiązania optymalne stanowią współrzędne punktów A i B, czyli x\ = 2000 szt. i x*2 = 4000 szt. lub x\ = 4000 szt. i x\ = 2000 szt. Łatwo sprawdzić, że wartość funkcji celu w obu przypadkach wynosi 6000.

Przykład 3. Przedsiębiorstwo produkuje cztery wyroby: W_l5 W₂, W₃ i W₄. Dwa spośród wielu środków używanych w procesie produkcji są limitowane. Limity te wynoszą: środek 1 - 90 0000 jedn., natomiast środek II - 120000 jedn. Nakłady limitowanych środków na jednostkę produkcji podano w tabl. 3.

Tablica 3

Środki	Jednostkowe nakłady
produkcji		w2	w3	W4
I	1	2	1,5	6
II	2	2	1,5	4

Zysk osiągany na jednostce produkcji kształtuje się odpowiednio: 4, 6, 3 i 12 zł. Ustalić optymalne rozmiary produkcji poszczególnych wyrobów. Podać łączny zysk zrealizowany przy optymalnym asortymencie produkcji:

Rozwiązanie. Niech x_v x₂, x₃ i x₄ oznaczają odpowiednio liczbę wyrobów W_l5 W₂, W₃ i W₄. Model dla wyżej przedstawionego zadania ma postać:

X, +2x₂ + 1,5jc₃ + 6x₄< 90000,

(1)

(2)

(3)

2x₁ + 2x₁+ 1,5x3 + 4    120000,

x₁>0,    x₂^0,    x₃^0,    x₄^0,

(4)    F(x₁,x₂,x₃,x₄) = 4x₁ -t-6x₂ + 3x₃ +12 -*• max.

Powyższy model nazywać będziemy programem pierwotnym (w skrócie PP). W dalszej kolejności zbudujemy 1 program dualny] (w skrócie PD) względem PP. W programie dualnym będziemylmeli tyle zmiennych, ile występowało warunków ograniczających w PP. Ponieważ w PP występowały dwa warunki ograniczające, w PD znajdą się zatem dwie zmienne. Niech to będą zmienne y_x i y₂. W PD wystąpi tyle warunków ograniczających, ile było zmiennych decyzyjnych w PP, tj. cztery. W warunkach PD należy dokonać zmiany nierówności na przeciwne. Rolę parametrów funkcji celu PD pełnić będą ograniczenia z PP, tj. liczby 90000 i 120000. Funkcja celu w PP była maksymalizowana, a zatem funkcja celu w PD będzie minimalizowana.

Program dualny przybierze postać:

(1)

(2)

(3)

(4)

(5)

(6)

yi+2y₂ S* 4, 2>'i + 2 y₂ St 6, 1.5JT +1,5^ > 3, 6yx+4y₂ ^ 12,

y i>0,    y₂^0,

G(y₁,y₂) = 90000yj + IŻOOOO}^-* min.

Jak można łatwo zauważyć, program ten można rozwiązać metodą geometryczną ze względu na wymiary zadania (4 x 2) w przeciwieństwie do PP, którego ze względu na wymiary (2 x 4) nie można było rozwiązać tą metodą.

Rozwiązanie PD pokazano na rys. 4. Rozwiązanie to stanowią współrzędne punktu A, czyli

y\ = 2 oraz y\ = 1.    G(y\,y₂) = 300000.

W dalszej kolejności należy sprawdzić, w jaki sposób optymalne rozwiązanie PD spełnia warunki (l)-(4) PD. Po podstawieniu optymalnych wartości zmiennych PD stwierdzamy, że warunki (1) i (2) są słabo spełnione (zachodzi równość), a warunki (3) i (4) są ostro spełnione (zachodzi nierówność ostra). Stąd wniosek, że zmienne w PP o numerze 3 i 4 (czyli x₃ i x₄) są równe zeru. Tak więc dla rozwiązania PP można napisać układ równań:

Xj + 2x₂ = 90000, 2x_t + 2x₂ = 120000.

17