MATEMATYKA008

8 I Wiadomo&ci wstępne
j) |sinx|^Ot ł) |sinx-l|śl.
k) |x'-5cosx|>~2, 1)|x|<x2-2,
m) |l — logx|> 0, n) |31og(4-x:)-ctgx
>-l
Odpowiedzi:
1. a) fałszywe, b) prawdziwe, c) fałszywe, d) prawdziwe, e) prawdziwe. 0 fałszywo 3. a) fałszywe, b) prawdziwe, c) prawdziwe, d) prawdziwo, e) fałszywe, 0 fałszywe 5,o) UAn-<-2,2>.r|An-<-I.I>. bJUA.rf-w.+ooJ.DA.-łO}.
on li
7 a)xc(-l,4), b) X€(-oo,-I>u<5,+»).c) xe<-l,3>,d) X60, e)xeR.
0 x«kx,k€C, g) x€(1,3). h) xeR, i) x€0, j) x«kx,kcC, k) xeK,
1) xe(-so,-2)u(2,+<io), ł) xe<2kic,(2k r|)x>,keC, m) xc(0,l0)v^(10,+oo), ti) xe(-2,0)u(0,2).
2. LICZBY ZESPOLONE.
Określenie zbioru liczb zespolonych, weźmy
pod uwagę produkt kartezjański zbioru liczb rzeczywistych przez siebie, Izn. zbiór wszystkich uporządkowanych par (x,y) liczb rzeczywistych:
RxR = {(x,y): xgR a yeR}.
Z warunku uporządkowania wynika, źc równość par (x,,y,) i (x,,y;) zachodzi jedynie wtedy, gdy ich poprzedniki są równe i następniki są równe, czy li
(2.1) (x,,y,) = (Xj,yJ) o (x, =Xj a y,-y,).
W zbiorze RxR definiujemy dodawanie i mnożenie dowolnych elementów (x,,y,) i (x2,y2) tego zbioru za pomocą równości:
def
(2.2) (x,,y,) + (Xj,y2) = (x,+x,, y,+y2),
def
(2.3) (x,,y,)(x!,yJ) = (x,x: — y,y2, x,yj+ylxi)
Zbiór RxR z działaniami określonymi powyższymi równościami nazywamy zbiorem liczb zespolonych i oznaczamy literą C. a elementy z = (x,y) zbioru € nazywamy liczbami zespolonymi.
Liczby zespolone będziemy również oznaczać krócej pojedynczymi literami np.: z, w.
Z definicji (2.2) i (2.3) dodawania i mnożenia liczb zespolonych oraz z własności działań na liczbach rzeczywistych wynika natychmiast, że dla dowolnych liczb zespolonych z,,7.3,2, zachodzą równości
z, + z3 = z2 +Z,
Z|Z3=Z2Z,
(z,+z,) + z, = z, + (z, + z,) (z,z2)z, = z,(z2z,)
(z, +Z2)z, = z,z, + z,z3
przemienność dodawania pnemienność mnożenia
łączność Jodowania łączność mnożenia rozdzielność mnożenia wzylędem dodawana
ODEJMOWANIE I DZIELENIE LICZB ZESPOLONYCH
Odejmowanie i dzielenie liczb zespolonych definiujemy jako działania odwrotne do dodawania 1 mnożenia.
Łatwo wykazać, że dla dowolnej pary liczb zespolonych z, i z.2 istnieje dokładnie jedna liczba w taka, że z, = w + z2. Liczbę w nazy wamy różnicą liczb z, i z2 i oznaczamy symbolem z, - z2. Zatem
def
(z,-z2=w) o (z, -w + z2).
Analogicznie: dla dowolnej pary liczb zespolonych z, i z2 , gdy z2 *(0,0), istnieje dokładnie jedna liczba w taka, że z, = w z2 . Liczbę w nazy wamy ilorazem liczb z, i z, i oznaczamy symbolem
z,:z2 lub -- Zatem, przy założeniu, że z2 *(0,0) mamy Z2
Z def
(-■La. W) O (Z, = WZj).
Z2
Jeżeli z, =(x,,y1). z2-(x2,y2), to z przyjętych wyżej definicji otrzymujemy:
z,-zJ=(Xi-x„yl-yJ),
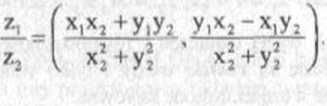
Wyszukiwarka
Podobne podstrony:
MATEMATYKA006 4 I Wiadomo.ici wstępne Produktem (iloczynem) kartezjańskim A xB zbiorów A i B nazywam
MATEMATYKA007 6 1 Wiadomości wstępne c)
MATEMATYKA023 I. Wiadomości wstępne FUNKCJE WYMIERNE. Funkcja wymierna jest to iloraz dwóch wielomia
MATEMATYKA 2(1) WZORY RACHUNKU RÓŻNICZKOWEGO [f(x)+g(x
Radosław Grzymkowski MATEMATYKA Zadania I Odpowiedzi Strona 3 Pochodna Funkcji fikcji Sl Pocho
IMGp48 1/ fll /ii AUoowout t)Orib£idiVci ;juę ^aUniiOPiOlr-Ót-Y ! v<k*h> li c^csdtorsiróffU
6 UięerCOUODOiy aiomatyczne t)C/tl t 5 " H= ?/*W A^ u^ Xiv ci^U3 «^u/, OrWl ót^j t^u /»L t U (&
więcej podobnych podstron