MATEMATYKA174

3 n VI Ciągi i szeregi funkcyjne

o^(x-l)^:+y² <^x² + y² <=> (x-1)² + y² <x² +y²o

o \>- <=> Rez>~.

Szereg jest więc zbieżny w każdym punkcie półplaszczyny Rcz>i ma sumę równą z - 1.

b)    Dla z*0 mamy |q)<l <=> |-—1<1 o |i+2|<|z|    |zJ>V5.

Szereg jesi więc zbieżny na zewnątrz okręgu o środku w punkcie z₀-0

i promieniu r=>/5. Suma tego szeregu jest równa -——

z~\—z

c) Ponieważ lq|<l <=> 1^-|<1    |z-2|<2, więc szereg jest

zbieżny dla każdego z spełniającego warunek )z-2|<2, czyli wewnątrz okręgu o środku Zq = 2 i promieniu r = 2. Suma tego szeregu jest równa

Izi    ■

z

PRZYKŁAD 5.3 Obliczymy promień zbieżności szeregu potęgowego:

Dla każdego z szeregów obliczamy jedną z granic-

limi^iaj,

iw*

lim&di

iw* a„

a) Ponieważ

lim^/W = IimJ-l^--=4,

» ^w «*»V n -f 3

więc r = 1/4; szereg jest zbieżny dla \Ą< 1/4₁ a rozbieżny dla |z|> 1/4. b) Ponieważ

limj^^atLł= lim -    se lim —-=0,

n ><*• a₀ n »*(n+l)! n-»*n + l

więc r = +<*; szereg jest zbieżny dla każdego zeC

limc/jajs lim>/nⁿ =

■wo.

więc r=0; szereg jesl zbieżny jedynie dla z-*0.    I

PRZYKŁAD 5.4 Wykażemy jednostajną zbieżność szeregu

£(nY) ¹ dla|z(il

O-l

Dla wyrazów' tego szeregu prawdziwe są nierówności

Ponicw^raż szereg liczbowy , jako harmoniczny rzędu a = 2, jest

zbieżny, więc badany szereg funkcyjny, na mocy kryterium Weierstrassa.

jest jednostajnie zbieżny dla Iz) > 1.

c) Ponieważ

FUNKCJE e\ co$z,sinz. Dla funkcji wykładniczej c* oraz funkcji trygonometrycznych cosx,sinx mamy następujące rozwinięcia Maclaurina dla x e R:

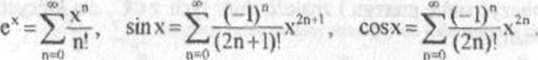
Przez analogię z tymi wzorami można określić funkcje e*. cosz, sin z zmiennej zespolonej z za pomocą równości

Promieniem zbieżności każdego z tych szeregów potęgowych jest r = +oo, zatem lak określone funkcje: wykładnicza i trygonometryczne są funkcjami ciągłymi na całej płaszczyźnie zespolonej Podstawiając w pierwszej