matma 12 20103

ityczna w przestrzeni

punkty)

Słliniowe punkty Pi =

Równania prostej

129

punkty.

kty P = (0,1,2), Q = (0,5,4), P₄ = (5,3,1)

ikładu współrzędnych na postać:

zczyzny.

o Ćwiczenie 5.5.11

a)    Znaleźć równanie płaszczyzny, która przechodzi przez punkt P — ( — 1,2,3) i odcina na osiacłi układu odcinki jednakowej długości. Ile rozwiązań ma to zadanie ?

b)    Obliczyć objętość czworościanu ograniczonego płaszczyzną ir : x + 2y 1-?>z —6 = 0 oraz płaszczyznami układu współrzędnych.

5.6 Równania prostej

• Fakt 5.6.1 (równanie parametryczne prostej)

Równanie prostej l przechodzącej przez punkt Po = (xo,yo,zo) o wektorze wodzącym ro i wyznaczonej przez niezerowy wektor kierunku v = (a,b,c) (rys. 5.6.1) ma postać:

l : r — ro + tv, gdzie t 6 R lub po rozpisaniu na współrzędne:

l ■ (x, V, z) = (*o, 2/o, za) + t(a, b, c), gdzie t <E IR.

Powyższą zależność nazywamy równaniem parametrycznym prostej w postaci wektorowej. Inny zapis tego równania ma postać

l

x = xq + at,

y = yo + bt,    gdzie t G

z = zo + ct,

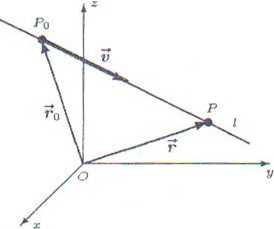
Rys. 5.6.1. Prosta wyznaczona przez punkt i wektor.

Uwaga. Powyższe równania będą przedstawiały półproste lub odcinek, gdy parametr t będzie przebiegał odpowiednio przedziały (—oo,/3], [a, oo) lub [a, 3\.

o Ćwiczenie 5.6.2

a)    Napisać równanie parametryczne prostej przechodzącej przez punkt Po = (—1,0,3) i równoległej do wektora v = (2, —1,5);

b)    Napisać równanie parametryczne prostej przechodzącej przez punkty P = (1,2,3), Q= (3,2,1).

1