matma 12 20104

130

Fakt 5.6.3 (równanie kierunkowe prostej)

Równanie prostej l przechodzącej przez punkt Po = (2:0, Vo, zo) i wyznaczonej przez niezerowy wektor kierunku v= (a, 6, c) (rys. 5.6.2) ma postać:

l :

x -x₀ y - ijo z - z₀

Geometria analityczna w przestrzeni

Równania prostej

• Definicja 5.6.6 (równi Prostą f, która jest częś

B\y + C\z + D\ =0,

zapisywać w postaci:

a    b    c

Ten sposób zapisu równania parametrycznego prostej nazywamy jej równaniem kierunkowym.

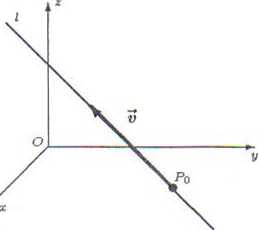
Rys. 5.6.2. Prosta l przechodzi przez punkt Po i jest równoległa do wektora v.

Uwaga. Aby nie ograniczać zakresu stosowania równania kierunkowego prostej przyjmujemy, że w mianownikach powyższych ułamków mogą wystąpić zera.

O Ćwiczenie 5.6.4

a) Wyznaczyć wektor kierunkowy prostej l : 4(x — 1) = 3(y + 2) = 2(3 — z);

x — 1 y + 2 z — 5

b)    Znaleźć punkty przecięcia prostej l układu współrzędnych;

c)    Zbadać, czy proste

1

z płaszczyznami

Ten sposób zapisu pros

*

Rys. 5.6,

Faktb.b.T^Ć o wektor z Wektor kierunkowy pr

h

x - 1 y + 2 2 ~ -1

.z

3’

z + 1 y + 11 z + 1

mają punkt wspólny.

O Ćwiczenie 5.6.5

a)    Z punktu S = (—30,50,0) w kierunku wyznaczonym przez wektor k = (3,4,12) wystrzelono rakietę z szybkością v = 1.3. Po jakim czasie rakieta będzie w odległości d = 150 od punktu obserwacyjnego O — (0,0,0)?

Uwaga. Współrzędne punktów podane są w km, a prędkość w km/s.

b)    Samolot zwiadowczy i rakieta poruszają się po prostych ze stałymi prędkościami. W chwili źi=0 samolot był .w punkcie Sj = (1,2,3), a w chwili t₂ = 3 w punkcie 5o = (—1,5,3). Natomiast rakietę, wystrzeloną w chwili t\ = 1 z punktu R\ = (0,0,0), zaobserwowano w punkcie Ro — (5,3, 2) w chwili <₂ = 4. Czy samolot zostanie trafiony przez rakietę?

ma postać

O Ćwiczenie 5.6.8

. _    , f 6z +

a) Prostą l : j _{3x +}

b)    Znaleźć punkt prz

c)    Zbadać, dla jakiej gdzie t £ M, przeć

d)    Zbadać, dla jakiej równoległa do pla

'. Ni 1 JL

1), =(*•>! %,».)■ , p, =

& - (Tń - r*

Oo_-e

T" —

x - ><w    _ y- v«=

X, ~ Xc

y rio