49043 matma 12 20105

131

Równania prostej

Definicja 5.6.6 (równanie krawędziowe prostej)

Prostą Z. która jest częścią wspólną dwóch nierównoleglych płaszczyzn ttj : Ayx-\-B\V + C'i² + D\ =0, 7r-2 : A₂x + B₂y + C22 -t- D₂ = 0 (rys. 5.6.3), będziemy zapisywać w postaci:

l

A\X + Biy -f C\Z + Di = 0, A₂x -ł- B₂y + C₂z + D₂ — 0.

Ten sposób zapisu prostej nazywamy jej równaniem krawędziowym.

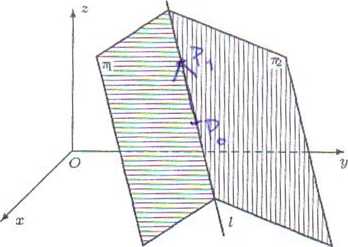
Rys. 5.6.3. Prosta jako część wspólna dwóch płaszczyzn.

¹ Fakt 5.6.7 (o wektorze kierunkowym prostej w postaci krawędziowej) Wektor kierunkowy prostej

f A\x + B\y + C\Z + Di = 0, ( A₂x T B₂y ~f~ C₂z T D₂ = 0

ma postać

—•)    ---j

■V 'p P

O 1

v — pi, B±,CiJx £A₂, B₂, C2J.

i

I

o Ćwiczenie 5.6.8i

\ o 1 f ;6a; +2y — z — 9 = 0,    .,    . /    A i ' t

a; Prostą l : |^2^ | 2~ — 12 - 0 ^zaP^{lsac w} P^ost,acl|P^arametry^czneJ>| {ła€. n<

b)    Znaleźć punkt przecięcia prostej l : i    z+2~Q ^z płaszczyzną xOz\

c)    Zbadać, dla jakiej wartości parametru m prosta l : x = 1 + 2t, y = —2, z = 31,

| x — 2y + z + rn = 0,

gdzie t S R, przecina prostą k

x -\-y — 2 + 3 = 0;

- py - z + 1 = 0,

jest

d) Zbadać, dla jakiej wartości parametru p prosta l : |    ^py t-__0

równoległa do płaszczyzny w : 3x + py + 2z — 1 = 0.