62068 matma 12 20106

132    Geometria analityczna w przestrzeni

Wzajemne położenia

5.7 Wzajemne położenia punktów, prostych i płaszczyzn

Definicja 5.7.1 (rzut punktu na płaszczyznę i na prostą)

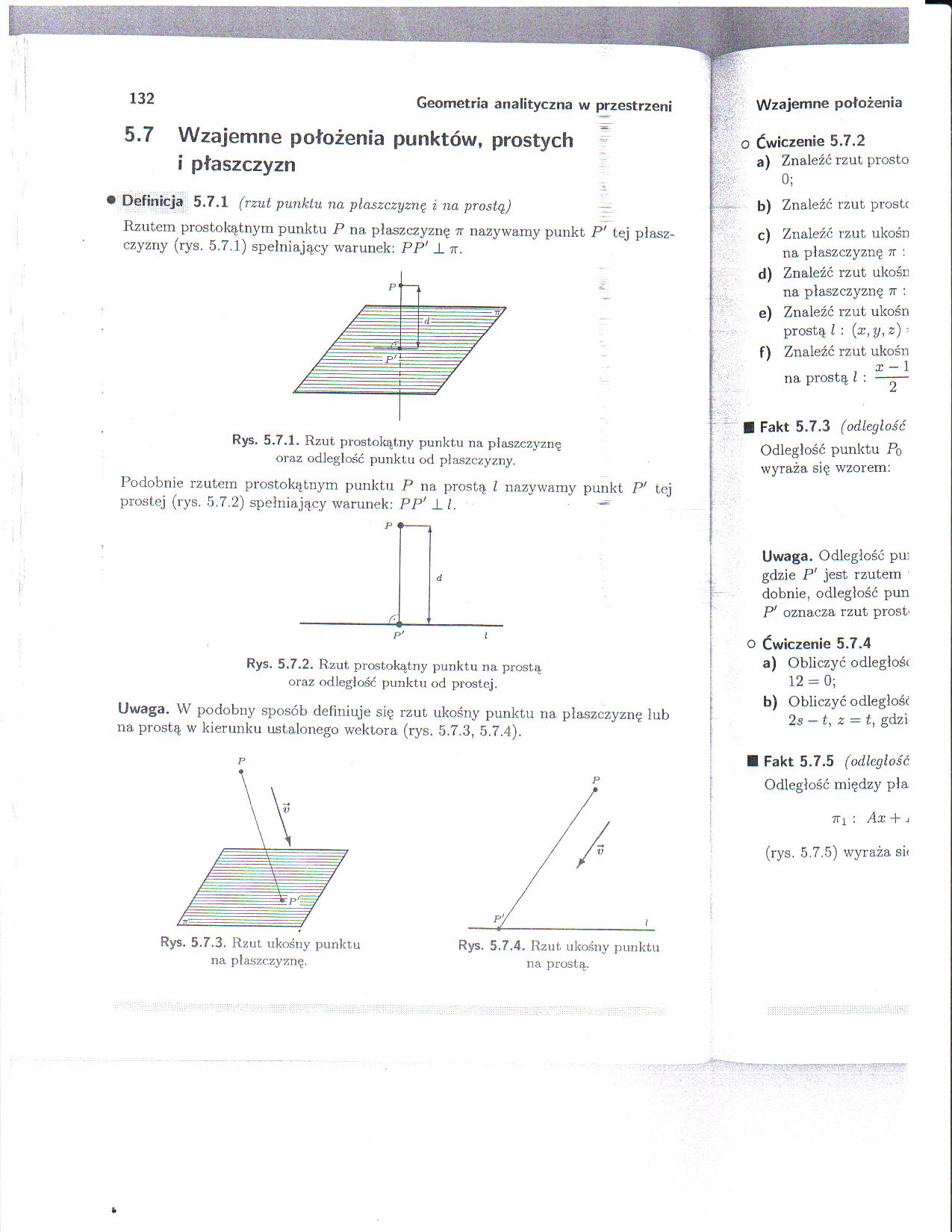
Rzutem prostokątnym punktu P na płaszczyznę tt nazywamy punkt P' tej płaszczyzny (rys. 5.7.1) spełniający warunek: PP' ± tt.

mh

o Ćwiczenie 5.7.2

a)    Znaleźć rzut prosto

0;

b)    Znaleźć rzut proste

c)

Rys. 5.7.1. Rzut. prostokątny punktu na płaszczyznę oraz odległość punktu od płaszczyzny.

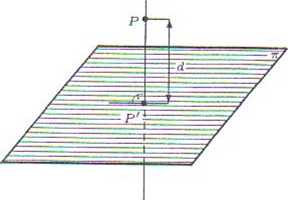
Podobnie rzutem prostokątnym punktu P na prostą. I nazywamy punkt P' tej prostej (rys. 5.7.2) spełniający warunek: PP' _L /.    —

p i

Znaleźć rzut ukośn na płaszczyznę n :

d)    Znaleźć rzut ukośn na płaszczyznę 7r :

e)    Znaleźć rzut ukośn prostą l : (ar, y, z) ■

f)    Znaleźć rzut ukośn

X — 1

na prostą l : ——

I Fakt 5.7.3 (odległość

Odległość punktu Po wyraża się wzorem:

p'

Rys. 5.7.2. Rzut prostokątny punktu na prostą oraz odległość punktu od prostej.

Uwaga. W podobny sposób definiuje się rzut ukośny punktu na płaszczyznę lub na prostą w kierunku ustalonego wektora (rys. 5.7.3, 5.7.4).

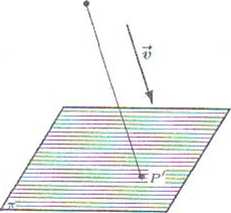
Rys. 5.7.3. Rzut ukośny punktu na płaszczyznę.

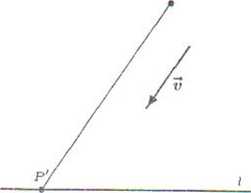
Rys. 5.7.4. Rzut ukośny punktu na prostą.

Uwaga. Odległość pu: gdzie P' jest rzutem dobnie, odległość pun P' oznacza rzut prost

O Ćwiczenie 5.7.4

a)    Obliczyć odległość

12 = 0;

b)    Obliczyć odległość 2s-t, z = t, gdzi

■ Fakt 5.7.5 (odległość Odległość między pła

tri : At + i

(rys. 5.7.5) wyraża sic

rrt»yyy.