miary rozproszenia (1)

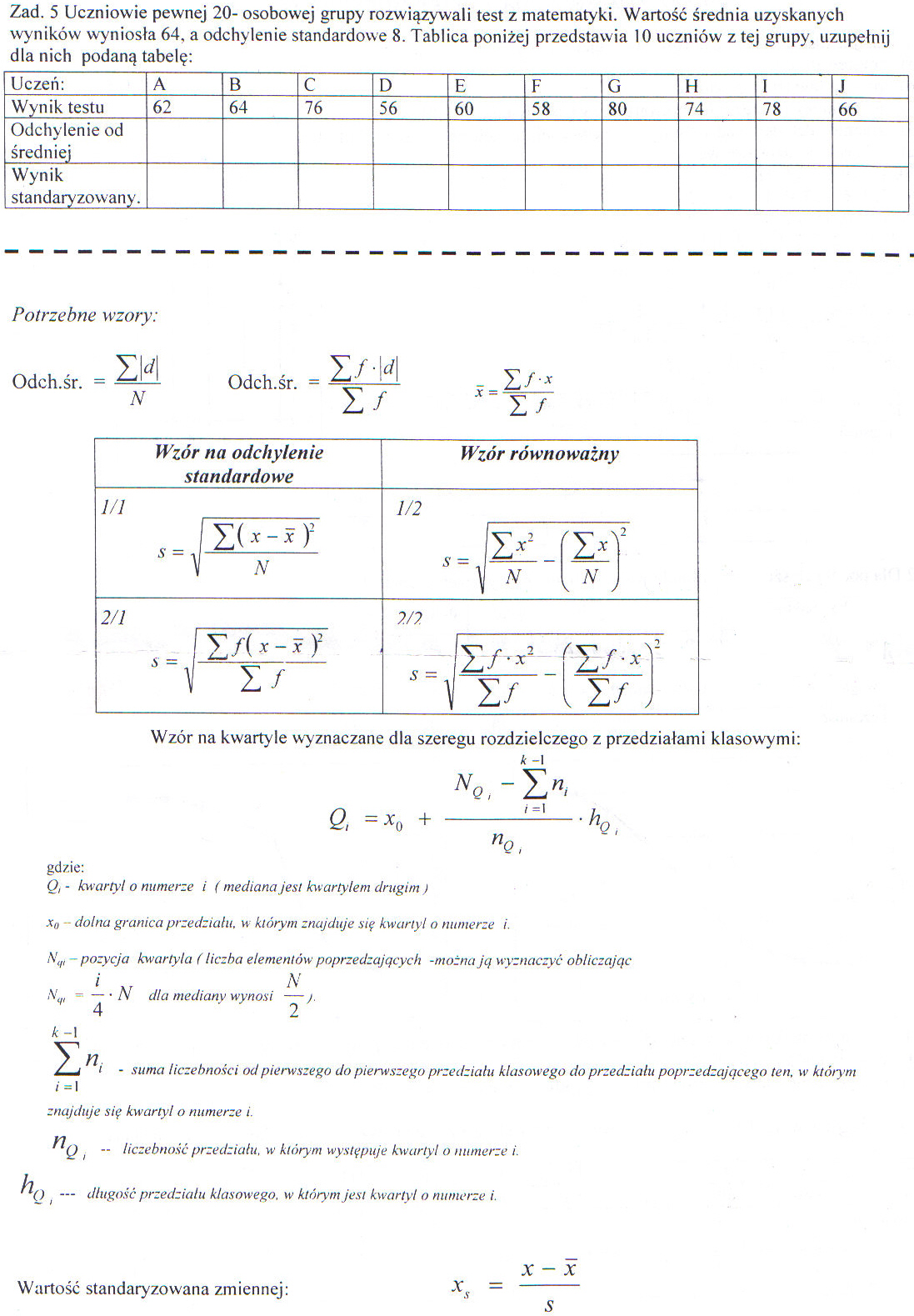
Zad. 5 Uczniowie pewnej 20- osobowej grupy rozwiązywali test z matematyki. Wartość średnia uzyskanych wyników wyniosła 64, a odchylenie standardowe 8. Tablica poniżej przedstawia 10 uczniów z tej grupy, uzupełnij dla nich podaną tabelę:

Uczeń:	A	B	C	D	E	F	G	H	I	J
Wynik testu	62	64	76	56	60	58	80	74	78	66
Odchylenie od średniej
Wynik standaryzowany.

Potrzebne wzory:

Odch.śr. =    Odch.śr. =    ^    - Z/'*

^N    1/    TT

Wzór na kwartyle wyznaczane dla szeregu rozdzielczego z przedziałami klasowymi:

k -i

^Ne,~'Lⁿi

Q, = *o +

ż=i

• K

n

Q,

Wzór na odchylenie standardowe	Wzór równoważny
1/1	1/2 s
-Pr^7		_ Z*^21	\^2 2> k ^N )
2/1	7/7
YAx-xy i/ ~	^S-\	Z/T	'■£/•* Y
		1/	l Z/ i

gdzie:

O, - kwarty I o numerze i ( mediana jest kwartylem drugim )

x₀ - dolna granica przedziału, w którym znajduje się kwartyl o numerze i.

A'_</( - pozycja kwartyla < liczba elementów poprzedzających -można ją wyznaczyć obliczając

i    N

N_t/, ~ — • A dla mediany wynosi —).

k -1

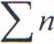
i - suma liczebności od pierwszego do pierwszego przedziału klasowego do przedziału poprzedzającego ten, w ktńiym i = I

znajduje się kwartyi o numerze i.

u

' ‘Q _l — liczebność przedziału, w którym występuje kwartyl o numerze i.

\j , — długość przedziału klasowego, w którym jest kwartyl o numerze i.

X ~ X

Wartość standaryzowana zmiennej:

5