new 65 (2)

132 7. Zasady obliczeń wytrzymałościowych śrub

W przypadku połączenia śruby dwustronnej z nagwintowanym gniazdem korpusu można przyjąć D « oo. Wówczas powyższy wzór przyjmie postać

1

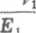
w

(7.17)

Gdy materiał śruby i korpusu jest taki sam (E₁ — E₂ = E, n = v₂) wzór (7.17) ma postać

Moment skręcający M, jaki trzeba przyłożyć, aby dokonać połączenia, wynika z sił tarcia na bocznych powierzchniach gwintu. Nacisk p„ na tych powierzchniach (rys. 7.12) jest równy

P

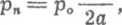
(7.19)

gdzie P — jest podziałką gwintu, aa — rzutem boku gwintu na oś.

W gwincie metrycznym P/2a = 8/5, gdzie p„ = 8p₀/5. Powierzchnia

Tv    . 2 i    .

tarcia jednego zwoju gwintu wynosi F = 2 — (d²—di)/cos — ; (oznaczenia podano na rys. 7.12).

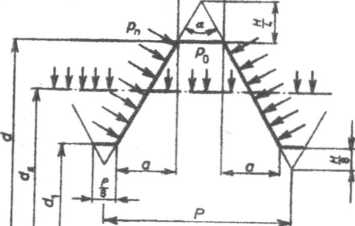
Rys. 7.12. Nacisk na bocznych powierzchniach gwintu pasowanego ciasno

Siła tarcia przy n zwojach gwintu na długości skręcenia i współczynniku tarcia // jest równa T = jup_nF„, a stąd moment tarcia

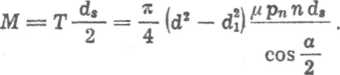
(7.20)

Warunek wytrzymałości dla śrub poddanych działaniu sił osiowych Q t Jednoczesnym skręcaniem momentem M według hipotezy Hubera określa nierówność

Oz =

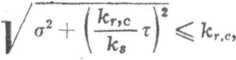
(7.21)

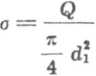
naprężeniem rozciąga

gdzie o_z Jest naprężeniem zastępczym,

jącym lub ściskającym, z — naprężeniem skręcającym, ak, i k_r>c są dopuszczalnymi naprężeniami przy skręcaniu oraz przy rozciąganiu k_T lub ściskaniu k_c, dj jest średnicą wewnętrzną gwintu śruby.

Zasady określania dopuszczalnych naprężeń podano w punkcie 7.2.

k

Przy obciążeniu statycznym “- — 1,7 (hipoteza Hubera) wzór (7.21)

K*

ma postać

(7.22)

o, = J ^Ao² + 3t² ^ k_r>c.

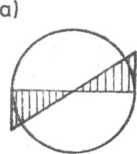
Naprężenia skręcające w zakresie odkształceń sprężystych (rys. 7.13a) wyznacza się ze wzoru

__ M

* ,3 '    (7.23)

18*

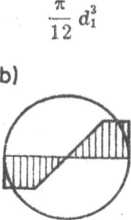
Jeśli w całym przekroju rdzenia śruby zachodzą odkształcenia plastyczne (rys. 7.13c), naprężenia skręcające są równe

M

T — -

(7.24)

Rys. 7.13. Rozkład naprężeń skręcających w śrubie: a) w zakresie odkształceń sprężystych, b) w zakresie odkształceń sprężysto-płastycznych, c) w zakresie odkształceń plastycznych

W tym przypadku zachodzi równość

]/ o^+lir² = R_e,    (7.25)

gdzie R, jest granicą plastyczności.