new 73 (2)

148

7. Zasady obliczeń wytrzymałościowych śrub

żenie robocze Q_r, to śruba będzie obciążona inną, mniejszą siłą zacisku Q_w (punkt A"), bowiem po plastycznym umocnieniu śruby, relacje między siłą i odkształceniem stają się liniowe zarówno przy odciążeniu jak i następnym dociążeniu.

Różnica między pierwotną siłą zacisku wstępnego Q_w i siłą zacisku po pierwszym i następnym cyklu zmian obciążenia Q_w jest równa

,    =    U    (7.59)

Ci~rCjj

gdzie d_pi jest trwałym przyrostem odkształcenia śruby w wyniku wzrostu obciążenia od wartości Q,„ do wartości Q₀.

7.5.2. Obliczenie sztywności śrub

Sztywność długich śrub o stałym przekroju dostatecznie dokładnie określa wzór

^Cl = ~f~⁼ ~^E\^F~ •    ⁽⁷⁶⁰⁾

°i    n

gdzie Q jest obciążeniem śruby, ó_x — odkształceniem wywołanym siłą Q, Ei — modułem sprężystości materiału śruby, F_x — polem przekroju poprzecznego, li — łączną grubością ściskanych elementów (długością rozciąganą śruby).

Gdy śruba ma na długości złącza różne średnice, jej sztywność jest równa

Ci =

_Q_

Q

E,

v qim y

(7.61)

§

i^i F, i

F,ł

Pole przekroju gwintu przyjmuje się równe

, _ d+d_t

^s 2

jest średnią średnicą gwintu.

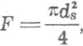
gdzie

Przy dokładniejszych obliczeniach śrub krótkich (l <C 6cł) należy uwzględniać odkształcenia gwintu śruby i nakrętki d_g oraz ewentualne odkształcenia łba śruby d_t.

Łączne odkształcenie będzie wtedy równe

di

E_[

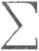
Im

+ 5, +a«.

(7.62)

I

Sumaryczne przemieszczenie dolnego najbardziej obciążonego zwoju gwintu d_a na podstawie wzorów (6.16), (6.17) i (6.22) jest równe

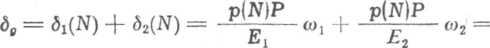
q(N)P² I

(7.63)

K ds t_n \

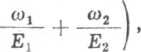
gdzie q(N) jest liniowym obciążeniem dolnego zwoju, P — podzialką gwintu, d, — średnią średnicą roboczą gwintu, t„ — głębokością nośną gwintu, wi i o)₂ współczynnikami bezwymiarowymi.

Przyjmując dla dostatecznie wysokiej nakrętki ctghmN = 1 i zgodnie ze wzorem (6.33) obciążenie liniowe q(N) — Qm, oraz wyrażając m zależnością (6.28), otrzymujemy wzór (7.63) w postaci gdzie f\ i F, są polami przekrojów poprzecznych śruiby i nakrętki. Gdy materiał śruby i nakrętki jest taki sam (E₁ — E₂ = E), wzór ten po uproszczeniu przedstawia się następująco

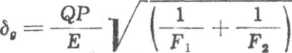
to, + w 2

(7.65)

W praktycznych inżynierskich obliczeniach (nieco mniej dokładnych) dla gwintowi metrycznych wykorzystuje się wzór wyznaczony na drodze doświadczało ej

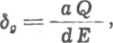
(7.66)

gdzie a jest bezwymiarowym współczynnikiem zależnym od stosunku średnicy nominalnej gwintu do podziałki. Przyjmuje się o = 0,8-1-0,95

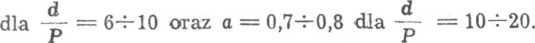
Podatność łba śruby jest niewielka i w praktycznych obliczeniach na ogół pomijalna. Uwzględnia się ją jedynie w obliczeniach dokładnych śrub krótkich z niskimi łbami. Dominującym odkształceniem łba jest ugięcie wywołane ścinaniem. Przy założeniu, że średnia średnica oporowa łba jest równa l,4d odkształcenia te są równe

gdzie h jest wysokością łba.

W niektórych przypadkach dla zmniejszenia sztywności śruby stosuje się w złączu elementy sprężyste (rys. 7.25). Odkształcenie sprężyste tych elementów oblicza się ze wzoru