new 82 (2)

168 7. Zasady obliczeń wytrzymałościowych śrub

Ou>

Et

>

(7.105)

gdzie E_t jest modułem sprężystości materiału śruby w temperaturze T.

Odkształcenie to wobec przyjętego założenia (E —> oo) — jest niezmienne w czasie. Ale pod wpływem pełzania w śrubie następuje przyrost odkształceń trwałych de_p, wobec czego przyrost odkształceń sprężystych de, musi być ujemny, tak by spełniony był warunek

(7.106)

de = dfp+de, — 0.

Dzieląc wszystkie wyrazy równania przez przyrost czasu dt, otrzymujemy

-^d-P- ₊ jj?«_ = v_ + dt ⁺ dt    ^

a na podstawie zależności (7.104) mamy

do

do

Erdt

(7.107)

Erdt

= 0.

(7.108)

Rozdzielając zmienne i całkując od zera do t, otrzymujemy

Ś-S--$

B(t)E_rdt

(7.109)

lub, wprowadzając uśrednioną wartość współczynnika B tak by spełniony

t

był warunek Bt —) B(t)dt,

(7.110)

Y^(o¹-^m-o¹ur^m) = ~E_TBt.

Stąd po przekształceniu

o

O to

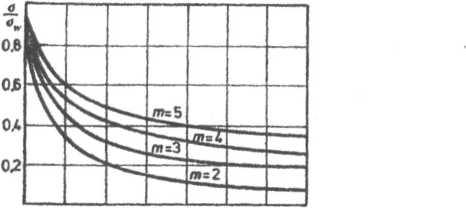
0    2 A 6    8    10    12 f" Rys. 7.45. Relaksacja naprężeń w śrubie

(7.111)

Na rysunku 7.45 przedstawiono zależność bezwymiarowej funkcji Mprężeń określonej równaniem (7.111) od bezwymiarowego czasu

(7.112)

Jak wynika z wykresu szczególnie szybki spadek naprężeń (a więc i obciążenia wstępnego) występuje w początkowym okresie pracy.

Uwzględnienie pełzania elementów łączonych prowadzi do zależności (patrz wzór (7.108))

(7.113)

We wzorze tym indeks 1 odnosi się do śruby, a 2 do łączonych elementów.

Wprowadzając uśrednione wartości współczynników Bj i B₂ oraz uwzględniając, że a_lF₁ = o₂F₂ otrzymamy po przekształceniu

der

0\

)_ — /D l D f? \

¹ l¹ 2 F?)

/ *iti + EiFi

Scałkowanie tego równania prowadzi do wzoru

dt.

(7.114)

= [l + (m-l)t*]

i

1—m

(7.115)

gdzie:

(» > B \ EyE_iF_i l ¹ B'^ł F? I E₁F₁ + E₂F₂

(7.116)

F? /    -rv₂r₂

Jeśli w zespole elementów łączonych znajduje się element sprężysty o bardzo dużej podatności (E₂    0), to t* -*■ 0 i w śrubie naprężenia

pozostają niezmienne a_} — a_w.

7.5.6. Obliczenie wytrzymałości śrub

Zasada obliczeń i określania naprężeń dopuszczalnych śrub statycznie obciążonych jest tama sama jak dla śrub rozciąganych i skręcanych bez zacisku wstępnego. Warunek wytrzymałości określa wzór (7.22), w któ-

Qc

rym naprężenie rozciągające a ——ji-oblicza się dla maksymalnej siły

4

Q_c, natomiast naprężenie skręcające r——-—dla momentu dokręcenia

“uT

M = 0,5(3,^, tg (y + g') — wywołanego siłą zacisku wstępnego Q_w- Jest