P1010854 (2)

336 x liski

Po ■lamtaoi s*iy rozporowej H dla różnych i siniejących -dzajdn obeiąM ^

zooaie wmości statyczne w dowolnym przekroju łuku od ległym o wartość x od — wmmej podpory obbczzmy według następujących wzorów ab poprzeczni

ab normalna

Q_J,‘=Q₀,cotf-ff sin 9,

m

aa

mirr nr rgnająry

OM

pkae Q*m i '^4« — ab poprzeczna j moment jak dla belki prostej wolnopodpartcj «pre-kroją odległym ar od podpory w danym przypadku (rys. 7,12), o - kąt nacN^HmM aej do Mu v danym puakeic względem poziomej.

L- 'aku o kaztaśae paraboŁ drugiego stopnia kąt y lub jego modna tJdbcryŁ ze wzorów

V.

sin ęm -    ^ —

9

oM

(7.18)

a

2

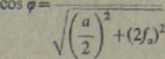
znaczenia a i f, podano na rys. 7.13.

Dla punktu po drugiej stronie osi symetrii łuku wartości sinus i cosinus znajdujemy w/orów trygonometrycznych

sin(-p)-—sin p, cos(— p)<«cos <f.

Należy zaznaczyć, że zwykle działanie sił poprzecznych Q„ w przekrojach hiku poluje niewielkie naprężenia ścinające, przeto może być w obliczeniach pominięte. Gotowe wzory do obliczania łuków trójprzepbowych i dwuprzegubowych dla różnych Wypadków obciążeń podano w tablicach 61 i 62, natomiast dla łuków bezprzegubowych | tablicach 63 i 64.

»Ł3. Łuki trójprzegubowe

Łuk trójprzegubowy jest układem statycznie wyznaczalnym. Pod wpływem obciążeń nętrznych występują w łuku siły styczne normalne oraz momenty zginające, na które daruje się przekroje łuku. W łukach trójprzegubowych zmiany temperatury i skurcz nu nie wpływają na wielkości statyczne.

Do wyznaczania czterech niewiadomych podporowych w łuku trójprzegubowym mamy lępujące równania:

1)    £J=0 - suma składowych poziomych,

2)    J)y=0 - suma składowych pionowych,

3)    —    suma    momentów    względem    punktu    B,

L    —    suma    momentów    względem    punktu    A,

14j    -    suma    momentów    względem    punktu    C.

■. Analityczne obliczenie łuku trójpizegubowego, obciążonego siłami skupionymi (rys. B4) przeprowadzono poniżej.

■ Z równania £2T«0 wynika, że

(7.19)

Bodową pionową reakcji w punkcie A obliczamy z równania momentów względem

iktu B

(7.20)

abnic z równania £ 3/^-0 możemy obliczyć R% lub wprost z równania £K«Q, stąd jnnamy

lenatruleeje batonowa