p1080120

istnieje odwzorowanie wzajemnie jednoznaczne jednego zbioru wtedy, fidy każdemu elementowi jtuasszegO-zbMW prr)iw«|dkQKany_jaL «lQU^iS£^cnc^enr^iooudaiycg<u_każdy element drugtego' J* obm^mty^TćSiwgo ciernemu zbioru pierwszego. Sytuację taką przedstawia

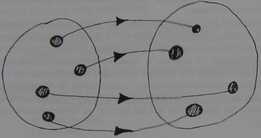
R)». 33

rysunek:    *

Następne rysunki przedstawiają dla odmiany zbiory nicrównolic/nc.

Równoliczność można ustalać oczywiście w inny sposób, np. na poziomic enaktywnym - przez łączenie w pary. nakładanie elementów, otaczanie pętelkami itd.. można również stosować inne niż strzałkowe schematy graficzne. Gdy wyobrazimy sobie rozmaite zbiory skończone, to można wśród nich zauważyć zbiory równolśczne. mające po 2 elementy, po S elementów, po 14 elementów itp. Wspólną własnością zbiorów równolicznych (abstrahujemy od rodzaju przedmiotów. koloru, wielkości, kształtu itd.) jest liczba naturalna. W praktyce szkolnej, mając (np. na rysunku) 3 kwiatki. 3 jabłka. 3 kasztany. 3 liście itp., dziecko stwierdza, że zbiory pr zedmiotów są równoliczne. że wszystkiego jest po 3. wspólną cechą tych zbiorów jest to. że mają po 3 elementy. Określając liczbę

elementów danego obioru, dochodzimydo aspektu kardynał nciO łigby natural-juij, który przesadnie akcentowano w reformach nauczania matematyki pod koniec lat sześćdziesiątych. Liczba kardynalna, oderwana od dziesiątkowego systemu numeracji, nk. powiązana z aspektem porządkowym, okazała się „niestrawna” dla dzieci. Niekorzystne okazało się uprzywilejowanie jednego aspektu pojęcia liczby naturalnej, ponieważ równie ważne są także pozostał: aspekty.

•W aspckęię .porządkowym liczby zwracamy uwagę na to który z koło danen; flaoggaz&dni jrw w danej chwilli    «y Ustawiając w szeregu

pczcdmioi^r porządkując je i num&ując, dziecko odpowiad.a.oą^pyianie; który z koki? czv też: ik tu iest? Liczba porządkowa, podobnie jak liczba kardynalna, odnosi się zawsze do jakiegoś zbioru. Na przykład gdy uczeń mówi: piąty zeszyt, piąty dzień, piąte jabłko, wówczas eksponuje aspekt porządkowy liczby 5.

U podstaw pojęcia liczby naturalnej jako liczby porządkowej leży pojęcie podobnego uporządkowania zbiorów. Przyjmujemy, że dwa zbiory liniowo uporządkowane (np. zbiór panów i pań tańczących poloneza) są równoliczne i spełniają następujący warunek: jeżeli demem a poprzedza element b w pierwszym zbiorze (pani a poprzedza panią b). to również odpowiednik elementu a poprzedza odpowiednik elementu b (pan tańczący z panią a poprzedza pana tańczącego z panią b) (Siwek 1992). Gdy mamy zbiory skończone dobrze uporządkowane, to - podobnie jak w wypadku zbiorów równolicznych - możemy wyróżnić wśród nich zbiory mające na przykład po 5. 10. 17 elementów. Ostatni element zbioru uporządkowanego liniowo.informuje^* wielkości lego ■zbiocu

■ _|V« W_nsnckcie miarowym Iję/ha traktowana jest iakn miara pewnei wielkości .uc¹' - ciągłej: długości, ciężaru, czasu. Na osi liczbowej na przykład dziecko może t1 zaznaczyć długość mierzoną krokami, wpisując liczby I, 2, 3, 4... itd. Aspekt .ci₍.. miarowy jest najtrudniejszy z rozważanych czterech aspektów. Przy pomiarach i l ₍ wielkości ciągłych pojawiają się bowiem trzy obiektywne trudności pojęciowe:

I ..Pomiar jest zawsze tylko przybliżony. Gdy mamy na przykład 5 jabłka, to rzeczywiście liczba jabłek jest dokładnie równa 3. Jeśli zaś mamy np. 3 litry mleka, to liczba 3 nic jest wartością absolutnie dokładną, może być jedynie określona w granicach błędu pomiaru.

2.    \Vvnik nomiaru może być liczba naturalna, ulaniem, lub-liczbą luew.y-ipicrną..

3.    Wvnik ńoriiinni zależy od wyboru iedńośłifi t_a sama wielkość ma przy różnych jednostkach oczywiście różne miary.

Aby przygotować dzieci do prawidłowego rozumienia pojęcia miary i pojęcia liczby naturalnej, warto używać w klasie zwrotów typu ..prawie pięć". „około pięć", „pięć i jeszcze trochę".

Trzeba stosować różne jednostki, np. długość stołu mierzyć za pomocą ołówka, patyczka, różnych klocków z zestawu Cuiscndre'* (kolorowych liczb).

237