PA300006

(1)

(2)

cos a =

OA

a+r

OD

^tgx=AD

1.24. I Dwie jednakowe gładkie kule o promieniu r i ciężarze Q każda 2av^J I szono na niciach o jednakowej długości a, tak jak pokazano na rys. a. Znaję.

I siły S w niciach oraz siły R wzajemnego nacisku kul na siebie.

.* Rozwiązanie. Siły działające na obie kule, po uwolnieniu kul od więzfy przedstawiono na rys. b. Jak widać, rozpatrywany układ jest symetryczny w _8t.’ sunku do płaszczyzny pionowej, a zatem dla znalezienia szukanych sił S i R vvyj

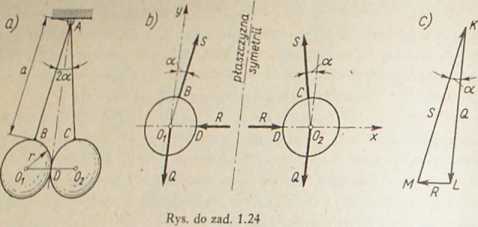
tarczy rozpatrzyć równowagę jednej tylko kuli, gdyż odpowiednie równania napisane dla kuli drugiej dadzą identyczne związki. Ponieważ układ sił działających na każdą z kul jest układem zbieżnym, przeto warunkiem pozostawania kul w równowadze jest aby dla każdej kuli sumy rzutów sil na nierównoległe osie x i y przyjętego układu współrzędnych były równe zeru. Warunki te napisane dla lewej kuli dadzą następu- , jące równania:

'    = Ssina—R = 0,    £~^P_iy = Scoscł~Q — 0.

Stąd

cos a

R — Ssina = Qtgoc.

Pozostaje do wyznaczenia kąt a. Z trójkąta OAD mamy AD j/(a+r)²—r² __ j/a(a-j-2r)

a+r

oraz

ya(a+2r)'

Pd podstawieniu powyższych wyrażeń do wzorów (1) i (2) otrzymamy ostatecznie

_s_ Q(^a+^r) 1 Qr

]/a(a+2r) ’    ]/a(a+2r)

owyższe wyrażenia uzyskać można w łatwy sposób, wykorzystując podobieństwo

5 a+r____a+r__a+r

Q " ^AD ~ |/(a+r)²—r* “ |/a(a+2r)

R___r__ r

Q ⁼ AD ~ y<*(a+2r) ’

skąd łatwo otrzymujemy wzory (1) i (2), uzyskane uprzednio z równań równowagi. 1.25.    Na dwa jednakowe gładkie walce o promieniach r i ciężarze G = 25 N

każdy, włożone do prostokątnej skrzyni, położono sześcian o Krawędzi a i ciężarze Q — 40 N, tak jak podano na rys. a. Określić nacisk sześcianu na walce oraz reakcje w punktach styczności walców ze ścianami i z dnem skrzyni. Tarcie pominąć.

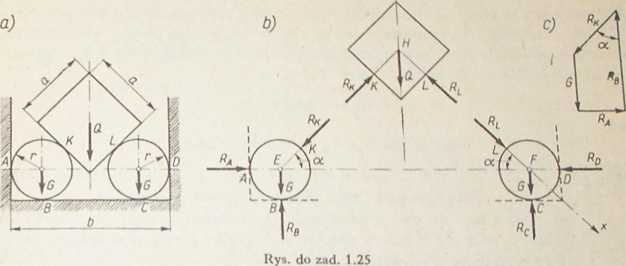
Rozwiązanie. Wyznaczenie nacisku sześcianu na walce oraz reakcji w punktach styku walców ze ścianami i dnem skrzyni jest możliwe jedynie wówczas, gdy każdą z części rozpatrywanego układu, tzn. zarówno sześcian jak i każdy z walców, rozpatrzymy — po uwolnieniu od więzów — jako ciała swobodne, na które działają, oprócz własnych sił ciężkości, jeszcze odpowiednie siły reakcji. Ponieważ walce są gładkie, siły reakcji we wszystkich punktach A, B, C i D styku walców ze skrzynią oraz w punktach K i L styku walców z sześcianem są normalne do bocznych powierzchni odpowiednich walców. Wynika stąd, że na każdy walec działają siły zbieżne których linie działania przecinają się w środku walca. Z uwagi na brak oporów tarci; na powierzchniach walców, sześcian — w warunkach równowagi — zajmuje taki położenie, że jego boczne powierzchnie tworzą z poziomem kąty 45°, a siły, jaki na niego działają, stanowią również układ zbieżny. Siły działające na sześcian i walc przedstawiono na rys. b. Wszystkie te siły działają w jednej płyszczyźnie, prost< padłej do podłużnych osi walców. Jak widać z rys. b, rozpatrywany układ jest s; metryczny względem płaszczyzny pionowej, a zatem odpowiadające sobie siły j obydwu stronach płaszczyzny symetrii są parami równe co do wartości liczbowy<j

Ra — Rd» Rb — Rc, Rjc — Rl •

TAI