PC043353

Rozdział 3. Funkcje¹ jednej zmiennej

c) Prosta v = jr jest asymptotą (dwustronną) wykresu f(x) = x + bowit

'    „ sinx

lim (f(x) - x) = lun -- O.

jt ,±eb    X *±co X

Natomiast prosta o równaniu x — 0 nie jest asymptotą pionową, gdyż lim]

x—*0l

(ma więc .skończoną wartość).

Przykład 3.28.

Funkcja f(x) = V.r² + I. x e R. jest ciągła; Jej wykres nie ma asymptot pionc Korzystając ze wzorów (3.10), wyznaczymy asymptoty ukośne. W przypadku asyn w —oo mamy

l t&T)    lxi f~T

a- lim —-= lim —\[1-+    = —1.

£-*^**> X    X V X²

Wyraz wolny w równaniu asymptoty jest równy

b = lim (VŹ3+~I+ x) = lim flxl-t/l +—=■+xl = lim -——..... -n

^v * '~~x(i₊jrrj)

Prosta o równaniu y = —x jest więc asymptotą wykresu funkcji f w -co. Analogicznie można pokazać, że asymptota w oo ma równanie y = x.

3.3.2. Ciągłość funkcji

Definicja 3.14.

Niech X c R. Funkcję f;X R nazywamy ciągłą w punkcie x₀ e X wtedy i tylko wtedy, gdy dla każdego zbieżnego do xo ciągu (x„) punktów zbioru X, ciąg (f(x„)) wartości funkcji jest zbieżny do f(xo).

Mówimy, że funkcja jest ciągła na zbiorze A c X wtedy i tylko wtedy, gdy jest ona ciągła w każdym punkcie tego zbioru.

Uwagi.

a)    Funkcję ciągłą na swojej dziedzinie (czyli na zbiorze X) będziemy nazywali po prostu funkcją ciągłą.

b)    Jeśli xo € X jest punktem skupienia zbioru X, to warunek podany w definicji 3.14 jest równoważny warunkowi

lim f(x)=f (.to).

X-*Xo

Warto zwrócić uwagę, że wyrazy ciągu (x„) mogą być równe xo. Dlatego można mówić o ciągłości funkcji w punktach izolowanych zbioru X

Co więcej, w każdym takim punkcie funkcja jest ciągła. W szczególności funkcja

dla x € (0, l), dla x = 2

jest ciągła także w punkcie x = 2.

Twierdzenie 3.19.

Suma, iloczyn, iloraz i złożenie (jeśli są określone) funkcji ciągłych są funkcjami ciągłymi.

Przykład 3.29.

Funkcja /(x) = x, x e R jest ciągła. Z tego faktu oraz z ostatniego twierdzenia wynika, że funkcja wielomianowa

gdzie flo,..., a* są ustalonymi liczbami, jest ciągła.

Twierdzenie 3.20.

Funkcje wielomianowe, wykładnicze, logarytmiczne oraz trygonometryczne są ciągłe.

Przykład 3.30.

Ż twierdzeń 3.19 oraz 3.20 wynika, że ciągła jest funkcja

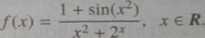
Funkcja odwrotna do funkcji ciągłej, nawet jeśli istnieje, nie musi być ciągła. Istotnie, na przykład funkcja

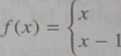
dla * < 0, dla x > 1

jest ciągła w każdym punkcie swojej dziedziny, tj. zbioru (—oo, 0) U Funkcja do niej odwrotna

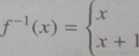
dla x < 0, dla x > 0

nie jest ciągła w punkcie x — 0.

Podamy kilka bardzo ważnych własności funkcji ciągłych, do których będziemy się odwoływać w kolejnych podrozdziałach.

117