PC043363

Rozdział 3. Funkcje jednej zmiennej

jest nieskończenie wiele razy różniczkowalna, w szczególności w punkcie x a q a jej pochodne wszystkich rzędów są równe w tym punkcie zeru, co można łaty pokazać.

Dla dowolnego x e R suma szeregu (3.22) jest równa zeru, a tym samym jest różna od f(x) dla x > 0. Równość (3.22) nie jest więc spełniona, ponieważ lim R„ (x,xq) # 0.

3.5. Rachunek całkowy 3.5.1. Całka nieoznaczona

Niech I będzie przedziałem otwartym, D — sumą pewnej liczby przedziałów otwartych.

(Definicja 3.21.

Funkcję F: D —* R nazywamy funkcją pierwotną funkcji /: D —* R wtedy i tylko wtedy, gdy F'(x) = f(x) dla x g D.

Przykład 3.53.

Wyznaczymy funkcje pierwotne F kilku wybranych funkcji /. a) Funkcją pierwotną funkcji f{x) = 0,xeR, jest każda funkcja stała, b) Funkcjami pierwotnymi funkcji f(x) = x, x e R, są np. fiinkje Fj(x) = |r, F₂(x) = 5# + 5 oraz F₃(x) = ±xr - 2.

c) Funkcją pierwotną /(x) = x # 0, jest np. funkcja F(x) = ln \x\. Istotnie, jefi x > 0, to (ln Wy = (lnx)' = Jeżeli natomiast x < 0, to z twierdzenia o pochodnej funkcji złożonej (twierdzenie 3.26) otrzymujemy (ln W)' = (ln(-x))' = -Jj = j.

Twierdzenie 339.

Jeśli F,G: I —* R są funkcjami pierwotnymi funkcji f: I -+ R, to istnieje taka liczba c € R, że F(x) = G(x) + c dla każdego x e I.

Założenie w ostatnim twierdzeniu, że dziedziną funkcji jest pojedynczy przedział jest istotne. Funkcjami pierwotnymi funkcji f(x) = x # 0 (określonej na sumie dwóch rozłącznych przedziałów) są funkcje

dla x > 0, dla x < 0.

F(x) = ln\x\, G(x) = |jⁿ ]*\ ⁺ t

{ln kl - 2

Nie jest natomiast prawdą, że F — G jest funkcją stałą na zbiorze R - {0}.

Twierdzenie 3.40.

Każda funkcja ciągła ma funkcję pierwotną.

Definicja 3.22.

Zbiór funkcji pierwotnych funkcji / nazywamy całką nieoznaczoną funkcji / i oznaczamy symbolem J f(x) cU.

Uwagi.

a)    Jeśli funkcja /, określona na pewnym przedziale, ma funkcję pierwotną, to można zapisać:

J f(x) dx = F(x) + c* F'(x) = /(*).

Każdy rezultat różniczkowania wyznacza wynik pewnego całkowania. Na przykład (sin² *)' = sin 2x oznacza, że J sin 2x dr = sin² x + c, gdzie xeR.

b)    W definicji 3.22, funkcję / nazywamy funkcją podcałkową, x - zmienną całkowania.

W poniższej tabeli przedstawiamy wzory na całki dla wybranych funkcji.

Funkcja /	/ f(x)dx	Uwagi
x°	(o*\)* ^TCr	a#-l
1	ln |x| + c	&
e*	e* + c
sin.r	- cos x + c
COSX	sinx + c "

Wzory rachunku różniczkowego mają swoje odpowiedniki w rachunku całkowym. Formułują je twierdzenia 3.41-3.43.

Twierdzenie 3.41.

Jeżeli funkcje f,g: I R mają funkcje pierwotne, to funkcje / + g oraz af, gdzie aeR, także mają funkcje pierwotne i zachodzą wzory:

Jcf(x) + g(x))dx = J f(x)dx + J g(x)dx, J af(x)dx = a J f(x)dx.

Przykład 3.54. Dla .r 0 mamy

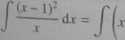
-2 +

- j dr = J'xdx-2^dx + J'^dr= ^.r-2x + lnM ^{+ c}-

137