PC043364

Rozdział 3. Funkcje jednej zmiennej

Ze wzoru na pochodną iloczynu (wv)' = u"v + uv' otrzymujemy następują-,

fakt.

Twierdzenie 3.42. (Twierdzenie o całkowaniu przez części)

Jeżeli funkcje f,g są różniczkowalne w sposób ciągły na D, to_

(321)

J* f(x)gf(x)dx = f(.x)g(x) - J' f'(x)g(x)dx.

Najważniejszy jest właściwy podział funkcji podcałkowej na f(x) oraz /(>) tak, aby po zastosowaniu wzoru (3.24) całka po prawej stronie równości (3Jf) była prostsza do wyznaczenia od wyjściowej. Trudno podać w tej materii ogólne zasady.

Przykład 3.55.

a) Wyznaczymy /x sin xdr. gdzie ar 6 R. Wybierzmy /(x) = x, g'(x) = sini. Wied; /'(ar) = I oraz g(x) = - cos ar. Ze wzoru (3.24) otrzymujemy

'-cosi)— / (— cosi)di * —icosi + sini + c.

b)    Obliczymy całkę J lnxdx, gdzie x > 0. Podstawiamy /(i) = Im oraz /(i) = L Mamy /'(x) = j i np. g(x) = x. Stąd otrzymujemy

J'lnidi = ilni-'idi =ilni-i + c,

c)    W przypadku całki f siaxcosxdx przyjmijmy /(x) = sin x, /(ar) = cosi. Zatem /'(i) = cosi i np. g(x) = sinx. Dlatego

W konsekwencji całka jest równa | sin² x + c, gdzie x € R.

Twierdzenie 3.43. (Twierdzenie o całkowaniu przez podstawienie)

Jeżeli funkcja / jest ciągła, g zaś - różniczkowało a w sposób ciągły, to

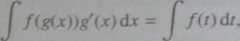
gdzie t = gtr) oraz di = /(jcjdr.

Przykład 3.56.    .

a) Wyznaczmy całkę /gf dx. Podstawimy t = sini. Mamy d; = (sinif" ' cosi di i dlatego całka ma postać

/COSI

sini

di =    - = ln (y| + c = In | sin x| + c,

oczywiście przy założeniu, że sin i # 0.

b) Niech a€ R. Podstawienie t — x - a (dr = Ar) prowadzi do wniosku. U

r dr r a/ ,

J = J — = lnW + c»lnU-ał + e.

c) Rozważania z dwóch ostatnich podpunktów łatwo uogólnić, rozważając całkę /    4*- Dokonując podstawienia t = /(z), mamy df = /'(r)dr I łatwo się prze

konać, że prawdziwy jest wzór

//w^dxshl^^wł+c'    ^(X25)

Jego prawdziwość możemy wykazać też bezpośrednio, różniczkując jego prawą stronę.

Funkcje wymierne są funkcjami postaci

^/w=H j|

gdzie P i 2 # 0 są odpowiednio wielomianami stopnia n i m.

Bez zmniejszenia ogólności rozważań, możemy przyjąć, żc n < m, gdyż w przeciwnym przypadku wystarczy podzielić licznik przez mianownik, aby otrzymać przedstawienie funkcji wymiernej w postaci sumy wielomianu i funkcji wymiernej, w której stopień licznika jest mniejszy od stopnia mianownika:

P(x)

Q(x)

= w(x) +

Pito

Q(x)'

gdzie w,P\ są wielomianami, przy czym st(w) = tt-rn, st(Pj) < st(Q). W ten sposób trudność całkowania funkcji wymiernej sprowadza się do całkowania takich funkcji wymiernych, dla których stopień licznika jest mniejszy od stopnia mianownika.

Definicja 3.23.

Ułamkami prostymi nazywamy funkcje postaci

A    Bx + C

(x — df' (ax² + bx + tf'

gdzie A, B, C, a,b,c są liczbami rzeczywistymi, k € N, natomiast trójmian ar+ bx + c nie ma pierwiastków rzeczywistych.

Twierdzenie 3.44.

Funkcja wymierna (3.26), gdzie P to wielomian stopnia mniejszego od stopnia wielomianu Q, jest sumą ułamków prostych, których mianowniki są dzielnikami fi.

139