P3040984

5.5 Nośność belek blsymetiycznych, homogenicznych

(6.19)

w którym:

Co — długość strefy ściskanej, którą należy przyjmować wg wzoru:

ę,*c + 5k,

(5.20)

c — długość elementu przekazująca bezpośrednio obciążenie. Długością (c) mośe być szerokość pasa belki lub elementu naroża przekazującego obciążenie ściskające. Wymiar (c) należy przyjmować wg zasad podanych na rys.5.12, k — suma grubości pasa tf i promienia wyokrąglenia (r) miedzy pasem a środnikiem. Wartości promieni (r) przekrojów belek walcowanych podane są w tablicach 191, ł» — grubość środnika belki, ą, — współczynnik, który należy obliczać wg wzoru:

(5.21)

o_c — naprężenia ściskające od zginania w środniku na krawędzi styku z pasem w zakresie 0.5 /tf 2    £ / j.

Nośność obliczeniową Pr, środnika belki spawanej obciążonego statyczną silą skupioną należy obliczać wg wzoru:

%=*e 4 fi.

(5.22)

gdzie:

k_r — współczynnik, który należy obliczać wg wzoru:

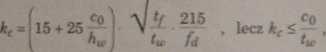
(5.23)

l_w, hu — grubość i wysokość środnika, tf — grubość pasa belki,

Co — długość strefy ściskanej, którą dla podstawowych przy

padków rozwiązań konstrukcyjnych (przekazywania obciążeń) należy przyjmować wg rys.5.13.

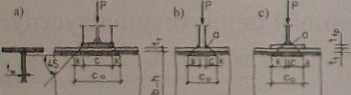
Rjf.5.13, Strefy wpływu obciążenia skupionego na trodnik belki spawanej

_| UśaisiJ

Jeśli elementem konstrukcyjnym, przekazującym obciążenie na zginaną belkę, będzie inna belka z poprzecznym żebrem usztywniającym jej środnik (rys.5.13a), to (*) obliczymy ze wzoru:

* = tf* t_w .

(5.24)

W przypadku, gdy belka podpierana jest spawana i bez poprzecznych żeber usztywniających jej środnik (rys.5.13c), to długość (*> możemy obliczyć wg wzoru:

r*orf»Mwy profłMowwiAi komtnJtctl mttttomyeh

gdzie:

In,i/y — pubaM tndnikł i pasa belki podpieranej, a — grubość spoin Ipmytli to elementy. tf — gruhcłC pasa botki podpierającej.

Przy obciążeniu botki sposobem Jak na ryaM.th. długość (ki można obliczyC «| wzoru:

(5.26)

Noźnoto Środnika pod obd^Moian skupionym miluty sprawdzić wg aa-Istno* ci P <    .

5.5.2. Nośność belki zginanej jednokierunkowo

Nratnnse betek zginanych jednokierunkowo natoky sprawdzać wg nant

t>Ł Wg

(5211

w którym:

M — maksymalny moment zginając? belką,

Mg — noknokC obliczeniowa przekroju, ęi_ — współczynnik zwichrzeniu, który najęły obtlezac wg zasad podanych w podrozdziale 6.3.

Współczynnik zwichrzenia % * l, jakh

□    belka jest konstrukcyjnio wystarczająco zabezpieczona przed zwichrzeniem,

□    belka jest zginana wzglądem mniejszej osi bezwladnokcl.

Nośność obliczeniową przekroju przy jednokierunkowym zginaniu Mg oblicza się sposobami rółnymi dla przekrojów klasy 1, S I 3, 4.

• Przekroje klas I. 3

Nośność obliczeniową przekrojów klasy I I 2 naloty obliczać wg wzoru:

Mg«<vW/V.

(B.2H)

w którym:

IV wtkaknik wytrzymałości przy zginaniu sprąłyslym dla skrajnych krawędzi przekroju,

cip — obliczeniowy współczynnik rezerwy plastycznej prsekro-jów pny zginaniu.

Do projektowania belek obciążonych tylko sutycznie obliczeniowy współczynnik rezerwy plastycznej przekroju motna przyjmować następująco:

(5.29)

w którym:

lVpj — jest wskaźnik lam oparu plastycznego pny zginaniu w stanie pełnego uplastycznienia.

Aby nastąpiło przystosowanie ślą przekroju belki w sianie uplastycz-nienia, winien być spełniony warunek A, = A, • 0,6 A, co oznacza, to współczynnik 15.29) można przyjmować tylko do przekrojów belek zginanych w ich płaszczyźnie symetrii. Wskaźnik oporu plastycznego mężna więc obliczyć wg wzoru.

WM IS.I *1*1 (6,30)