Scan0010

(p	0	I 6"	1 4*	1 7^71	1 2^71
Mg = —Pr sin (p	0	-{Pr	-O.lOlPr	-0,866Pr	-Pr
T = -Pcoscp	-P	-0,866P	—0,101 P	-V	0
N — -Psin©	0	-V	— 0,101 P	—0,866P	-P

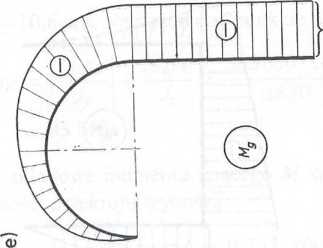
Wykresy sił wewnętrznych są przedstawione na rys. 8.9c, d i e.

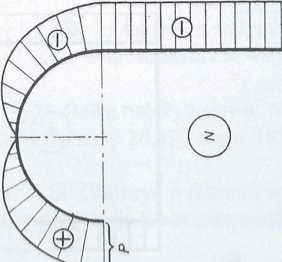
Zadanie 8.15. Wykonać wykresy sił wewnętrznych: sił normalnych N, sił tnących T i momentów gnących M» dla prętów przedstawionych na rys. 8. lOa i b.

ODPOWIEDŹ. Wykresy sił wewnętrznych dla pręta z rys. 8.10a pokazano na rys. 8.10c, d i e, a dla pręta z rys. 8.1 Ob —na rys. 8.10f, g i h.

Zadanie 8.16. Dla ram przedstawionych na rys. 8.1 la i b wykonać wykresy sił wewnętrznych: sił normalnych N, sił tnących T i momentów gnących M_g. ODPOWIEDŹ. Wykresy przedstawiono na rys. 8.1 lc-h.

Zadanie 8.17. Belka wspornikowa o długości / = 0.8 m jest obciążona na końcu pionową siłą P = 10 kN (rys. 8.12). Belka została wykonana z kątownika równoramiennego o wymiarach 150x150x20. Z tablic wyrobów hutniczych dla kątownika tego odczytano: e = 4,46 cm, J_yc =1154 cm⁴, J_y<r = 1830 cm⁴, J_z = = 480 cm⁴. Obliczyć największe naprężenie od zginania.

Rozwiązanie. Położenie przekroju poprzecznego belki względem siły obciążającej P podano na rys. 8.12. Najbardziej obciążonyjest przekrój belki w miejscu utwierdzenia, gdzie moment gnący osiąga wartość M_g — PI — 8000 N • m. Moment ten działa w płaszczyźnie pionowej, która w danym przypadku nie jest płaszczyzną główną belki. Osią główną przekroju jest oczywiście oś symetrii Cy_g, która tworzy z poziomą osią Cy_c kąt ao = 45°.

Mamy więc do czynienia ze zginaniem ukośnym. W takim przypadku oś obojętna nie jest prostopadła do płaszczyzny głównej centralnej, lecz tworzy z nią kąt /3q, określony wzorem

3,83

_{+ t} ^Jy_s i 1830 tgA> = tga_0;^ = ₁- —

skąd /-Jo = 75°.

Najhardziej oddalonym od osi obojętnej punktem pr/» kmju jt i punki k kio ropo współrzędne wyznaczone na podstawie rysunku, wwtns. a tI 1 ciii,

2 Pr

o