s 189

7.3. Przyspieszenie punktów ciała w ruchu płaskim

189

Korba 0 A obraca się ze stalą prędkością kątową co o- Znaleźć przyspieszenie punktu B mechanizmu, jeżeli korba O A zajmuje położenie poziome jak na rys. 7.49 oraz górne położenie pionowe (rys. 7.50). Dane: o)o, h, O A gg r, AB = 1.

\ Rozwiązanie

PRZYKŁAD 7.33

i

te

W położeniu poziomym (rys. 7.49) przyspieszenie punktu A mi tylko składową normalną

a_A = co²0r

Składowa normalna przyspieszenia punktu B

|1| = (o²AB\ to

Vą

OiA

<opr

VF^~h²

zatem

<Ą>r²l

l²-h²

Z warunku rzutów na oś y dostaniemy £ dfrl sin a — dfo! cos a = 0

M)

<Sz=^aBn'^lSa

Wk

M)

W-h²

(o^r²lh

l² - h² V/² - h² (/2 - h²)!

Przyspieszenie punktu B znajdujemy, rzutując trzy jego składowe na oś x

ag — —a_A — ajfa' cos a — sin a =

11,    r    rh² \

= —ra)Qt 1 ft v-f--"-¹ ,=    —r I

W płożeniu pionowym mechanizmu (rys. 7.50) chwili środek obrotu pręta A fi leży w nieskończoności, stąd i I czyli prędkość kątowa łącznika AB jest równa zeru, 110. Stąd przyspieszenie = 0.

I warunku rzutów

(j4)

—a a li a_Br cos a: = 0

■

JA) _ M _    _ toprt

°^Bt cosa BC //2 — (r + h)²

T

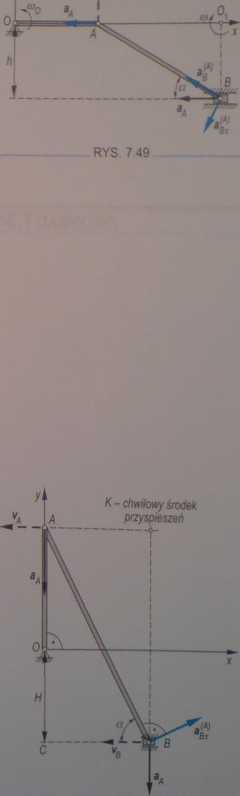
RYS. 7.50-