Scan Pic0034

więc:

IWl = NRT.

Przemiana ze stanu 2 do 3 jest izochoryczna (W= 0).

Rozwiązanie zadania 2.9 Prawidłowa odpowiedź: D.

Równanie stanu gazu informuje nas, że niezależnie od wartości poszczególnych parametrów, dla stałej masy gazu, zachodzi: vV

-^jŁ= const = NR,

T

gdzie N jest liczbą moli gazu.

Jeśli przemiana gazu jest izobaryczna {p = const), to:

V NR

— =-= const.

T V

Zależność objętości gazu od temperatury jest więc funkcją liniową:

y₌NR_T,

V

znaną z matematyki w postaci y = ax, gdzie współczynnik kierunkowy

jest równy a =

= tga, a a jest kątem nachylenia prostej

V

do osi T.

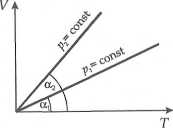
Jeśli więc przemiana izobaryczna jest przeprowadzona pod stałym, wysokim ciśnieniem p_v to

^:tg«i

ma wartość małą, jeśli zaś pod stałym lecz niskim ciśnieniem p₂, to

NR

tza-

Vi

ma dużą wartość.

W rozpatrywanym zadaniu wystarczy więc przez każdy z punktów 1, 2, 3, 4 przeprowadzić izobarę i sprawdzić, który kąt nachylenia jest najmniejszy (patrz rysunek obok).

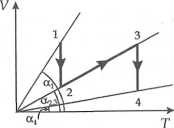
Rozwiązanie zadania 2.10 Prawidłowa odpowiedź: B. Przemiana: 1—*2 - izotermiczna

2— >3 - izochoryczna

3— A. - izobaryczna

Rozwiązanie zadania 2.11 Prawidłowa odpowiedź: D.

Dla przemiany izobarycznej 1—*2

Z wykresu widzimy, że V_l = V₃ i T₂ = T₃, V₂ = V₄. Dla przemiany 3—4

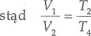
A zatem

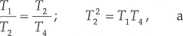
więc T₂ = JTJ₄ .

Rozwiązanie zadania 2.12 Prawidłowa odpowiedź: A.

Przy przejściu ze stanu K do stanu L wszystkie parametry ulegają zmianie:

Pk^vk ₌ Pl^vl T    T '

■*K    ¹L

ale T_l=2T_k i p_L=4p_K,'

więc

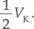
^Vk=^2Vl' oraz V_L =

Jeśli objętość danej masy gazu zmalała dwukrotnie, to gęstość gazu p{^p- dwukrotnie wzrosła.

- 67 -