skan0311

314 Elektrochemia

II prawo Ficka określa szybkość zmiany stężenia substancji dyfundującej w danym miejscu:

(6.100)

dc_Gx(A-, i)    d²c{x,t)

dt    dx²

W równaniach tych Z) oznacza współczynnik dyfuzji substancji dyfundującej. W tej postaci prawa Ficka są ważne dla tzw. dyfuzji seminieskończonej liniowej, w której substancja dyfunduje do płaskiej powierzchni znajdującej się wx = 0 po liniach prostych, prostopadłych do tej powierzchni. Rozwiązania praw Ficka prowadzą do czasowych zależności stężenia substancji w danym miejscu x.

Przykład 6.22. W oparciu o rozwiązanie II prawa Ficka przy warunku początkowym c(x, 0) = Cq (zob. Dodatek D2), obliczyć przepływ substancji J(x,t) w funkcji odległości x dla czasów t = 1 s, 10 s oraz 100 s. Przyjąć D = 1 • 10^-9 m² • s^-1 oraz c₀= 10 mol • mf³.

Rozwiązanie. Rozwiązaniem II prawa Ficka przy zadanych warunkach początkowym i brzegowym jest funkcja

^c(*’'^)=eo^erf(yfer)>

w której erf (y) oznacza funkcję błędu Gaussa

erf (y) =

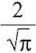
J exp (-ir)du. o

Zgodnie z I prawem Ficka obliczenie przepływu wymaga znajomości gradientu stężenia

J(x, t) = -D

dc(x, l) dx

Wykorzystamy tu podstawowe twierdzenie rachunku całkowego*^ - „całka oznaczona funkcji ciągłej ma pochodną względem górnej granicy całkowania, równą wartości, jaką przybiera funkcja podcałkowa, jeśli w miejsce zmiennej całkowania zostania wstawiona górna granica całkowania”

d f

— J f(u)du -f iy).

dv i

Zatem jeśli

2 y

F(y)= ~y~ J exp {-u²) du = c(x, t),

^(7t R. Lcitncr, Zarys matematyki wyższej. WNT, Warszawa 1969, III/78.