skanuj0002 (417)

164

Ćwiczenia laboratoryjne z fizyki

Należy znaleźć funkcję Q(t) spełniającą powyższe równanie. Równanie (21.3) można rozwiązać metodą rozdzielenia zmiennych czasu t i ładunku Q:

—dt = -Q——dQ    (21.4)

SN

Po scałkowaniu uzyskuje się:

-/ = J?Cln(^ “ E j + 5,    (21.5)

stąd

Q(t) — C\B₂ exp

t

Irć

(21.6)

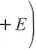
gdzie B_{ oraz B₂ są stałymi całkowania i spełniony jest związek B₂ = exp (—Ą ).

Aby określić stałą całkowania, należy wykorzystać warunki początkowe ładowania kondensatora. Ładunek na kondensatorze w chwili początkowej jest zerowy, tzn. Q(t = 0) = 0.

Stąd otrzymuje się:

Q(t) = CE l-exp

t

Jc

(21.7)

t

~RC

(21.8)

Natężenie prądu płynącego w obwodzie wynosi: _r/. dQ E

^,('⁾⁼1H^exp

a napięcie na ładowanym kondensatorze odpowiednio:

(21.9)

t

~RC

Wykładnik t/RC w równaniach (21.7), (21.8), (21.9) musi być bezwymiarowy, stąd wielkość RC ma wymiar czasu i nazywana jest stałą czasową obwodu. Jest ona równa czasowi, w jakim ładunek na kondensatorze powiększa się o czynnik (l-exp(-l)), czyli o około 63% swojej wartości w stanie równowagi. Prąd płynący w obwodzie spada w tym czasie do Ile swej wartości początkowej.

Po naładowaniu kondensatora klucz K zostaje przełączony do pozycji b (rys. 21.1), wówczas zachodzi rozładowanie kondensatora przez rezystancję R. W obwodzie brak siły elektromotorycznej (E = 0) i równanie (21.3) dla obwodu przyjmuje postać:

_ndQ Q _n i?—+ —= 0 dt C

(21.10)