skrypt055 (2)

JOS /.ubonitorluin /‘odstaw łHaktridtcfmlkl I

Jeżeli ubrałem jest elipsa, lak juk nu rys.6.5, lo kąt fazowy określa się ze wzoru (6.13) (w praktyce, w celu zwiększenia dokładności rozpatruje się odcinki dwa razy dłuższe yj i y2 niż OB i OA).

y

(p s* aresin-    (6.14)

Vmax

lilentylikacja waitości 0° lub 180° oraz 90° lub 270° jest możliwa gdy można zaobserwować kierunek kreślenia linii lub koia.

6.1.3. Rezystancyjny obwód prądu sinusoidalnego Gdy inipcdancja Z jest rezystancją:

Z = Rel^u    (6.15)

10 w obwodzie prądu sinusoidalnego obowiązują następujące relacje między skutecznymi zespolonymi wartościami prądu i napięcia:

11 = R-I    lub 1 = GU    (6.16)

Kąt fazowy <p=0° (prąd jest w fazie z napięciem), zaś moduł impedancji:

Z = R    (6.17)

Gdy dane są U oraz I, lo wartość rezystancji wynosi:

(6.18)

6.1.4. Indukcyjny obwód prądu sinusoidalnego

Gdy impedancja Z jest reaktancją indukcyjną:

Z- j m L=X], e^⁹⁰°    (6.19)

to w obwodzie prądu sinusoidalnego obowiązują następujące relacje między skutecznymi zespolonymi wartościami prądu i napięcia:

u-x_L.i-ci‘^J0<1

lub

[ = Hi -U e

-j-90°

(6.20)

Kąt fazowy cp=90° (napięcie wyprzedza prąd o 90°), zaś moduł impedancji jest równy wartości reaktancji indukcyjnej:

Z = X_L    (6.21)

Gdy dane są U oraz I, to wartość rcaktancji wynosi:

x_l=y

Stąd indukcyjność:

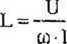
6.1.5. Pojemnościowy obwód prądu sinusoidalnego

Gdy impedancja Z. jest reaklancją pojemnościową:

1    _ i Qf|°

Z = -j--— = -e J⁹⁰    (6.24)

CO • L

to w obwodzie prądu sinusoidalnego obowiązują następujące relacje między skutecznymi zespolonymi wartościami prądu i napięcia:

U = X_Cd-t')'⁹⁰°    lub I=B_CU eJ'⁹⁰° (6.25)

Kąt fazowy (p=-90° (prąd wyprzedza napięcie o 90°), zaś impedancja rzeczywista jest równa wartości reaktancji pojemnościowej:

(6.26)

(6.27)

Z = X_C

Gdy dane są U oraz 1, to wartość reaktancji wynosi.

X_C^ ^u 1

Stąd pojemność: