Skrypt PKM 1 00075

150

R0ZWłĘZ3ⁿ*^e

2M

tg(y+ p0 +

= 22500 [N].

Obliczanie naprężco

<r, = ^ = 88,4 [N/mm²], 2iy/c_rE    . _ 1 rc

*■“ _l4ns;    ^a~ ii8o®'

**7VI

2i V^£ = ]    V«8.4 ‘ 21 ■ 10* = 75.2,

4/ /ff, 4-180 / 88,4

<*V£* 18 V2M0* ~^0,82’

tgfcę> =

sin h (p cos htp

sinfcfl»«(^-«**)-aS_f cos/ję> = («>* + «-*)• 0,5,

9 = 0,82,

«° ¹² _ g-0.82

unhę> = .---=0,915,

COahtp =

e^0M + e'⁰⁸²

1355,

*8*9 = 0,6752.

Naprężenia gnące

*•    0,6752

= 111,4 [N/mm¹].

Zadanie *4.5

a.    Obliczyć moment potrzebny do napięcia śruby z zad. 4.4 w trakcie montażu, jeżeli średnia średnica podparcia nakrętki D. = 25 [mm], P = 2,5 [mm]. </₂ = 18376 [mm], fi = 0,15 - współczynnik tarcia na gwincie i pod łbem nakrętki

b.    Wytłumaczyć, dlaczego napięcie śrub siłą Q = 0<6iF_tR_m przy sile naporu P_r= lF„R_m jest bezpieczne dla śruby (przy obciążeniach statycznych).

R_m — granica plastyczności k — 0,9 R_m - naprężenie dopuszczalne.

Rozwiązanie ad a.

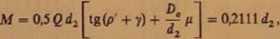
Af = 03111-22500-18,376 = 87381 [Nm].

ad b.

Zgodnie z wynikami z zad. 4.4 naprężenie w śrubach

o, «    = 0,6R_m -0,8R. < k.

P_t = 0,6 F_t i R,, + 03 F, i R_m = 03 F, i R_m.

Zadanie 4.6

Sporządzić wykres naprężeń zginających i rozciągających dla śruby dławnicy (zad. 4.4) w przekroju x = 0 i x=1 (rys. 4.10). Przyjąć dane z zad 4.4.

Rozwiązanie

Naprężenie skręcające