Skrypt PKM 1 00137

274

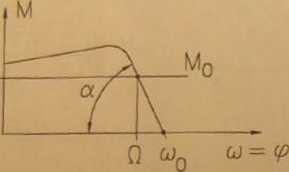
Łatwo zauważyć z rys. 8.12, żc p₀ jest proporcjonalne do tg a, gdzie a - kąt nachylenia charakterystyki statycznej silnika.

Układ równań (8.40). opisujący drgania swobodne, przyjmie obecnie postać

Po*o + c₀(*₀ - *) = 0,

J*_t+c₀(*-*₀) = 0.

(8.43)

Podstawiając

oraz

(8.44)

mamy

A₀{fip + Cjj) — Cg — 0,

-A₀c₀ + A_t{Jp* + c₀) = 0.

(8.45)

Przez przyrównanie wyznacznika głównego do zera otrzymujemy równanie na p. którego pierwiastki muszą przedstawiać drgania tłumione zarejestrowane w eksperymencie, tzn. że równanie

(8.46)

ma dwa pierwiastki zespolone, czyli

stąd

Pm = -a ±10.

Ostatecznie więc rozwiązaniem układu równań (8.40) będą funkcje •Po = A₀ e^-*' sin (rot + o*) + Ot + X₀,

(8.48)

(p = A,e~^mt sin (cór + a,) + Qi + A,.

Ostatnie z równań opisuje ruch wirnika silnika. Ponieważ częstość drgań swobodnych eksperymentu

5= ^=10 [1/s]

stałą c₀ można wyliczyć z relacji

-₂₌ęo_/_^V J \2fio) ‘

skąd

c₀ = 105 [Nmj

Odpowiedź:

Stałe modelu dynamicznego wynoszą p₀ = 20 [Nm/s], c₀ = 105 [Nm]. Na

skuteczność tłumienia przez silnik wpływa stała a =    . nachylenie charaktcrys-

² Po

tyki silnika związane jest ze stalą /?<>.

Zadanie 8.1 1

Jeżeli przyjąć założenie, spełnione w praktyce, że sztywność skrętna sprzęgła podatnego jest znacznie mniejsza niż sztywność pozostałych elementów napędu, to pracę sprzęgła podatnego z dobrym przybliżeniem opisuje model jak na rys. 8.13. Napisać równania ruchu względnego mas J_x i J₃ dla przypadku, gdy działa wymuszenie harmoniczne M = A/_Ocos(vr + *), a siła tłumiąca jest proporcjonalna do prędkości względnej x =    - <?,- Obliczyć amplitudę drgań ustalonych

oraz amplitudę drgań skrętnych w rezonansie.