70424 Skrypt PKM 1 00128

256

Przypadek wg rys. 8.1 c. Elementarny moment tarcia

dM_T = t - = pdFp    dF =    zdv.

Moment tarcia

dM_r — i - — pdFp - , dF=^dzdę>,

Moment tarcia

_    ^U 1 d    a« »    /A\2

M₀ = $dM_T = j jpn jp- j jpp(- J dzdip.

M₀ = ^tPlpp.

gdzie p jest średnim naciskiem na powierzchni czopa i wynosi

^p dr

stąd

(8.2)

Mo

Korzystając z wzorów (8.1) i (8.2) wyliczymy silę Q: ad b

Mo 850

ad. c

2 M

2-850

^Q nditi “ 3,14 0jD6 4 0.1 ~²^⁵'¹⁰* W]

Odpowiedź:

Każda ze śrub sprzęgła powinna dociskać pokrywy odpowiednio przy pasowaniu 0 60 H7/h6 siłą Q = 3,54 • 10* [N], a przy pasowaniu 0 60 H7/s6 siłą

2^5-10* [N].

Zadanie 8.2

Dwa wały o średnicy d dwupodporowc (każdy wał na dwóch łożyskach) są przesunięte równolegle o wartości c i w tej pozycji zamocowane do konstrukcji nośnej. Wały połączono za pomocą tarczowego sprzęgła sztywnego. Zakładając, że tylko jedno z czterech łożysk jest łożyskiem ustalającym, obliczyć moment zginający wał, a także stosunek e/d, jeżeli naprężenia zginające w wale nie mogą przekraczać wartości k = 50 [N/mm¹]. Do obliczeń przyjąć / = 5c = 1000 [mm], moduł sprężystości E = 2-10* [N/mm²], d = 50 [mm].

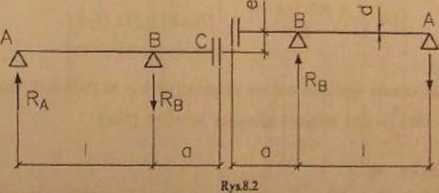
Rozwiąz.anie

Połączenie wałów wywoła ich zginanie, przy czym wał w miejscu połączenia sprzęgłem ugnie się o/oraz obróci o kąt O pod wpływem momentu zewnętrznego M. Ugięcia wałów z racji symetrii będą jednakowe i w sumie osiągną wartość e. stąd

/c+/o = 2/_C“« = 5^!<2! + 3o>.    <8J)

®^c = «»i>= 5^«+3o⁾.

Dla warunków zadania skupiony moment zginający

(8.4)

,,    3 EJ , n d*    „

^{M 9} 13 n^{1 r}* ^J~~64 ~ ^29,8 '^cm ^