spektroskopia043

86

niekrystalicznym stopem krzemu i GaAs. Jest to zrozumiałe, biorąc pod uwagę, że dawka 1 * 10¹⁶ cm^-2 daje efekt domieszkowania ok. 1-10²¹ cm^-3. Umieszczenie tak dużej liczby obcych atomów w sieci GaAs może także wprowadzić bardzo silne naprężenia wewnętrzne w tym związku oraz spowodować osłabienie wiązań Ga—As.

Metoda elipsometrii pozwala również kontrolować zmiany na powierzchni półprzewodnika spowodowane jej utlenianiem lub zdefektowaniem.

Elipsometria stała się szczególnie użyteczna do charakteryzacji złożonych związków i heterostruktur tworzonych z pierwiastków Ul grupy (In, Ga, Al) i Y grupy (As, Sb, P). Materiały takie znalazły szerokie zastosowanie w optoelektronice.

Funkcje dielektryczne związków A^Ga^^As, GaAsj.J?* są dobrze znane, a ich charakterystyczne parametry, takie jak pozycje energetyczne krawędzi i maksimów odpowiadających przejściom międzypasmo-wym, zależą od składu x. Dlatego pomiary elipsometryczne pozwalające wyznaczyć przebieg funkcji dielektrycznej są bardzo użyteczne do weryfikacji składu. Rysunek 49 przedstawia zależność e₂{hco) dla różnych składów aluminium. Widać, że ze wzrostem wartości x przejścia optyczne i E₁ + A₁ przesuwają się w kierunku większej energii.

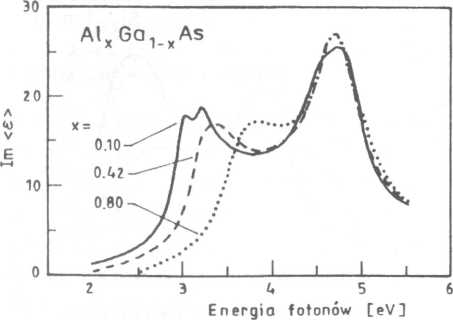
Rys. 49. Zależność spektralna części urojonej funkcji dielektrycznej Al*Ga, dla różnych zawartości aluminium [25]

Znając zależności E₁(x) i E_t -hd_l(x) możemy określić zawartość aluminium.

Badania heterostruktur półprzewodnikowych wykorzystujące elip-sometrię opierają się na metodzie zwanej modelem trzech ośrodków. Odpowiada to najprostszej heterostrukturze, tj. pojedynczej warstwie na podłożu o znanych parametrach. Padające światło przechodzi przez warstwę, której funkcję dielektryczną £, lub grubość d_t znamy, a następnie dociera do podłoża.

Dla takiego przypadku parametr p dla warstwy (1) na podłożu (2) w próżni (0) dla kąta padania $, przy założeniu braku warstwy przejściowej między warstwą a podłożem, ma postać [26]

(9-2)

₌ ^roi_P+^ri2_Pg'^2/,_ l+r_0l,r_l2te?²' l+^oi/u/'²' r_01j + r _12łe'^2/M

gdzie: r_ijp, r_iJs są współczynnikami odbicia (Fresnela) dla odbicia światła o polaryzacji p i s, odpowiednio na międzypowierzchni między ośrodkami i = 0, 1 oraz j = 1, 2.

Współczynniki Fresnela wyrażamy następująco:

(9.3)

(9.4)

_    £₀sin²^—e_lv/e_J—e₀sin²(P

^ip    £jy/£i — £₀sin²# + e, ^/ej—Eo sin² & ’

_ -Jei—e₀ sin² $—yfs_}—£₀ sin² $

^>js    ^e,—£₀sin²<P+ y/Ej—£₀sin²^’

gdzie: s₀, s_u s₂ — zespolone funkcje dielektryczne dla próżni (0), warstwy (1) i podłoża (2).

Przesunięcie fazowe /? ma postać

(9.5)

P = 2n jy/f,-E₀sin²<P,

gdzie X jest długością fali elektromagnetycznej w próżni.

Korzystając z wyrażeń określających funkcję dielektryczną s (9.1) oraz parametr p (9.2), możemy obliczyć efektywną funkcję dielektryczną <8> układu próżnia—warstwa—podłoże. Wyrażenie (9.2) określające p jest szczególnym przypadkiem wzoru dla przypadku wielowarstwowego [20].