SS854627

2

4. CEL ĆWICZENIA I ZAKRES BADAŃ

Dyskretny układ drgający o dwóch stopniach swobody jest najprostszym modelem, na którym można wykonać badania eksperymentalne oraz zaobserwować i z pewnym, nieuniknionym błędem wyznaczyć specyficzne własnośći układu i jego ruchu drgającego, o podstawowym znaczeniu w procesie projektowania nowych obiektów technicznych oraz modyfikacji konstrukcji obiektów już istniejących.

Podstawowym celem ćwiczenia jest doświadczalne potwierdzenie modeli i rozważań teoretycznych przedstawionych w kolejnym podrozdziale i pełniejsze zrozumienie zjawisk towarzyszących drganiom mechanicznym — wibracjom, które w znacznym zakresie można uogólnić dla drgań układów ciągłych.

Zakres badań obejmuje wyznaczenie postaci (modów) drgań, obliczenie naturalnych częstości drgań oraz porównanie ich wartości z wyznaczonymi w eksperymencie. Należy porównać postacie drgań wzbudzonych warunkami początkowymi odpowiadającymi obliczonym wektorom własnym układu

z postaciami drgań wzbudzonymi warunkami początkowymi różniącymi się od opisanych wektorami własnymi.

4.1. Wstęp teoretyczny

Równania drgań dyskretnych układów mechanicznych można wyznaczyć stosując zasadę

d’Alemberta. W przypadku układów o wielu stopniach swobody korzystniejsze jest posługiwanie się

równaniem Lagrange’a II rodzaju. Jeśli równania ruchu wyznaczane są dla współrzędnych odmierzanych w układzie bezwzględnym, z czym mamy w praktyce najczęściej do czynienia, najwygodniej jest przyjąć zapis macierzowy, w którym macierze tworzone są bezpośrednio na podstawie schematu układu drgającego. Do wniosków takich można dojść śledząc analizę przeprowadzoną dla modelu układu o dwóch stopniach swobody.

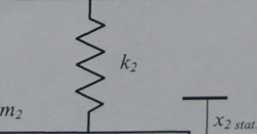
Do utworzenia równań ruchu drgającego na kierunku pionowym mas mj oraz m₂, rys. 4.1, zastosowane będzie równanie Lagrange’a II rodzaju

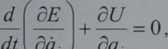
dtydąi) dq_f

mi

gdzie:

i =x_l(t) = x_l, q₂ =x₂{t) = x₂,

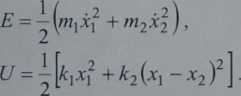
Współrzędne xj oraz X2 są odmierzane w układzie bezwzględnym. W zapisie uporządkowanym, ze względu na współrzędne ruchu oraz ich pochodne, różniczkowe równania ruchu przyjmują następującą formę

ki

stal.

Xi(t)

- X₂(t)

Rys. 4.1. Model układu o dwóch stopniach swobody

m{x\ + 0 • x₂ + (k\ + k₂ )*i + (—k₂ )x₂ = 0, 0 • Xi + m₂x₂ + (—k₂ )x_l + k₂x₂ = 0,

(4.1)