statystyka skrypt47

Świadczy też o tym wartość p ■ 0,0000, która jest mniejsza od przyjętej wartości poziomu istotności a. Do podobnego wniosku można dojść, biorąc pod uwagę obliczoną wartość statystyki F - 214,1409, która też znacznie przekracza wartość krytyczną Fo.os. i. s ■ 5,32 przy poziomie istotności a ■ 0,05 dla 1 stopnia swobody licznika i 8 stopni swobody mianownika (tablica U). Wartość statystyki t dla wyrazu wolnego równa jest t *= -0,77464 i jej bezwzględna wartość znacznie przekracza wartość krytyczną, co świadczy o tym, że wyraz wolny jest istotnie różny od zera.

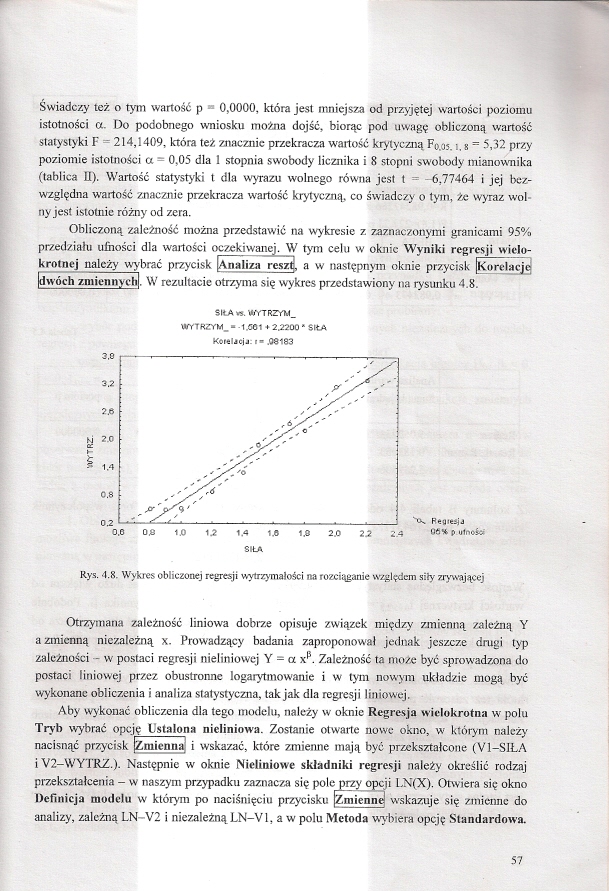
Obliczoną zależność można przedstawić na wykresie z zaznaczonymi granicami 95% przedziału ufności dla wartości oczekiwanej. W tym celu w oknie Wyniki regresji wielokrotnej należy wybrać przycisk [Analiza resztj a w następnym oknie przycisk |KorclacJc| (dwóch zmicnnycbl. W rezultacie otrzyma się wykres przedstawiony na rysunku 4.8.

SIŁA vi. VtfrTRZVM_ WTTRZYM. - -1.801 ♦ 2.2200■ SIŁA Konijc|j r- .06183

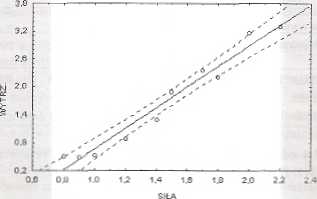
Ryt. 4.8. Wykres obbczooej regresji wytrzymałości na rozciąganie względem siły zrywającej

Otrzymana zależność liniowa dobrze opisuje związek między zmienną zależną Y a zmienną niezależną x. Prowadzący badania zaproponował jednak jeszcze drugi typ zależności - w postaci regresji nieliniowej Y = a x^p. Zależność ta może być sprowadzona do postaci liniowej przez obustronne logarytmowanie i w tym nowym układzie mogą być wykonane obliczenia i analiza statystyczna, tak jak dla regresji liniowej.

Aby wykonać obliczenia dla tego modelu, należy w oknie Regresja wielokrotna w polu Tryb wybrać opcję Ustalona nieliniowa. Zostanie otwarte nowe okno, w którym należy nacisnąć przycisk [Zmienna! i wskazać, które zmienne mają być przekształcone (V1-SILA i V2-WYTRZ.). Następnie w oknie Nieliniowe składniki regresji należy określić rodzaj przekształcenia - w naszym przypadku zaznacza się pole przy opcji LN(X). Otwiera się okno Definicja modelu w którym po naciśnięciu przycisku [Zmienne wskazuje się zmienne do analizy, zależną LN-V2 i niezależną LN-V1, a w polu Metoda wybiera opcję Standardowa.

57