Str132

25R Oflpiwiedięł do iłwfr/eń

14. (a) Złożeniem / «* P 4ó, (niod N) i C m / + h_t (mod A0 jest C •- p 4. /,

(mod JV), gdzie b « A, + Aj.

(b)    Złożeniem jest przekształcenie liniowe, w którym a — a_l • a₂.

(c)    Złożeniem jest przekształcenie afinicznc, w którym n = a_i • a. i A - a ₂ ó| 4- Ó2.

15.    P == 642C 4- 187 (mod 853); „DUMB IDEA ” (głupi pomysł).

16.    Najpierw oblicz / « 201C -f 250 (mod 881), a następnie P — 3317+ 257 (mod 757); „NO RETREAT” (nic ma odwrotu).

3.2

1. Słowem-kluczem szyfrującym jest słowo „SPY”. Tekst jawny (z odstępami i znakami przestankowymi umieszczonymi dla zwiększenia czytelności) brzmi następująco: „I had asked thal a cable from Washington to New Delhi summarizing the rcsults of the aid consortium be repeated to mc through the Toronto Consulate. It arrivcd in codę; no facilities cxisted for decoding. They brought it to me at the airport - a mass of numbers. I asked if they assumed I could read it. They said no. I asked how they managed. They said when something arrived in codę, they phoned Washington and had the original message read to them.” (John Kenneth Galb-raith, Ambassador’s Journal. Cytowane przez G. E. Mellena w „Cryptolo-gy, computers and common sense”, tom III Computers and Security.) (Poprosiłem, by depesza z Waszyngtonu podsumowująca decyzje rady do spraw pomocy była jeszcze raz wysłana przez Konsulat w Toronto. Przyszła zaszyfrowana; nie było żadnych możliwości rozszyfrowania. Przynieśli mi ją na lotnisko - było to mnóstwo liczb. Zapytałem, czy spodziewają się, że potrafię to odczytać. Odpowiedzieli, że nie. Zapytałem, w jaki sposób oni sobie zwykle radzą. Odpowiedzieli mi, że zawsze, gdy przychodzi jakaś zaszyfrowana wiadomość, dzwonią do Waszyngtonu i proszą, by im odczytano tekst oryginalny.)

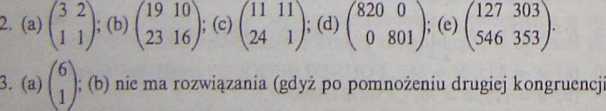
przez 2 i odjęciu od pierwszej dostajemy 6y = 8 (mod 9), co oznacza, że

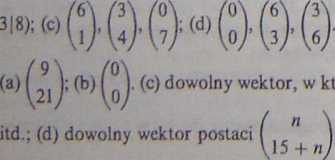
4.    ;órym x = y, tzn.

; (e) nie ma rozwiązania.

6. Zastosuj indukcję matematyczną, dowodząc trzy bezpośrednio dla n = 1, 2,..., /;, a następnie zakładając tezę dla n, udowodnij ją dla n + b. Oblicz mianowicie:

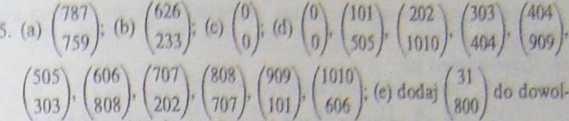
ncgo z 11 wektorów w (d) i zredukuj modulo 1)1).

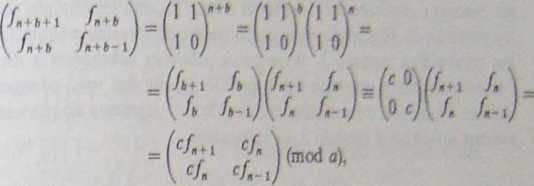
gdzie ce(Z/flZ)*, a następnie skorzystaj z założenia indukcyjnego. (Można dowieść, że dla dowolnej liczby całkowitej a istnieje liczba całkowita b taka, że a\f„ ob\n oraz że jeśli a = p* jest potęgą liczby pierwszej różnej od 5, to b jest dzielnikiem p^a~^l(p² - 1); dowód wykorzystuje pewne wiadomości z algebraicznej teorii liczb dotyczące ciała generowanego przez liczbę (V5 — l)/2 - zauważ, że ta liczba i liczba sprzężona z nią są wartościami własnymi macierzy w definicji liczb Fibonacciego.)

7. /I"¹ = fjjJ j\ „SENATORTOOK” (senator wziął).

^{i A} '^{L =} Ul 17 )> ”^{MEET AT N00N}” (spotkajmy się w południe).

20\

9.    A~^l = (17 ₀ , „WHY NO GO? MARIA” (dlaczego nie iść? Maria);

V2o o J

A = r j\ „JMLD W EFWJV”.

10.    „CJIABA KIICC”, co po rosyjsku znaczy „CHWAŁA KPZR” (KPZR - skrót nazwy Komunistyczna Partia Związku Radzieckiego).

11.    Złożenie systemów kryptograficznych ma macierz szyfrującą A₂A_V

, , . /18 28

12.    „?CVK”; najpierw pomnóż wektor kryptogramu przez macierz

(\    yI? aU

^ 2 I ^m0<^^u^⁰ 26; „STOP”.

13. Z twierdzenia 3.2.1 (z zaprzeczenia (b) wynika zaprzeczenie (c)) wynika, że istnieje niezerowy wektor przeprowadzany przez macierz A na wektor

Ten wektor tekstu jawnego może być dodany do dowolnego innego