str301

I S 5. POCHODNE TENSORÓW 301

Zadanie 5.4. Jak wiemy, składowymi kontrawariantnymi wektora prędkości są wielkości

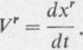
(1)

Jednak wyrażenia dVjdt nie są składowymi tensora i nie mogą przedstawiać przyspieszenia we współrzędnych krzywoliniowych. Wektorem kontrawariantnym przyspieszenia a^r jest pochodna absolutna wektora prędkości V, a mianowicie

(2)

a =

5V^r

17’

wobec czego możemy drugie prawo Newtona napisać w postaci

(3)

F^r = ma^r,

gdzie F^r jest kontrawariantnym wektorem siły działania, a m jest niezmienniczą masą.

Wyznaczyć składowe koncrawariantnego wektora siły działania we współrzędnych sferycznych x^l = g, x² = 0, x³ = ę, jeżeli dane są równania ruchu x^r(0 punktu materialnego o masie m.

Rozwiązanie. Korzystamy z wyników uzyskanych ze wzoru (5.2) w zadaniu 5.1, gdzie zostały wyznaczone składowe tensora

SV^_dT fr)    f r dtd

ot dt ⁺{msj dt dt^z ^{msj dt dt '

we współrzędnych sferycznych, mamy zatem

r d^2o	sin 20
U^2	2

F^l = m F² = m F³ = m

rd²(p    _nd0 dtp 2 dg d(p~\

I ^-T2'+2ctg ® ~T H--- ~7~'    •

| dt²    dt dt    g dt dfj

Zadanie 5.5. Dane są równania ruchu \*(t) punktu materialnego o masie m we współrzędnych cylindrycznych X¹ = r, x² = <p, x³ = z.

Wyznaczyć energię krytyczną T poruszającego się punktu materialnego, jeżeli wia-

domo, że
(1)	2 T = ma„mV^mV'
gdzie	. dx^k
(2)	^V =-J-* dt