str302

302 5. ZARYS RACHUNKU TENSOROWEGO

są składowymi kontrawariantnego wektora prędkości, a a_mn są składowymi tensora fundamentalnego przestrzeni. Wyznaczyć ponadto składowe kontrawariantnego wektora przyspieszenia

. 5V^k

<¹>

Rozwiązanie. Tensor metryczny a_mn we współrzędnych cylindrycznych ma składowe (patrz zad. 3.7).

(4)    a_mn = 0 dla m / n oraz a_u = 1,    a₂₁ = r²,    a₃₃ = 1.

Po uwzględnieniu zależności (2) i (4) we wzorze (1) otrzymujemy energię kinetyczną

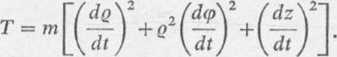
Składowe symbolu ChristolTela rodzaju drugiego we współrzędnych cylindrycznych przyjmują wartości (patrz zad. 4, §4):

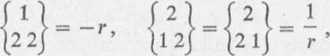
a wszystkie pozostałe składowe

Korzystając ze wzoru (5.2) oraz zależności (2) i (3) mamy

_{k    m}dx^s d^zx^k

^a    V -r---rr+

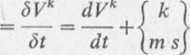
ym

dx^s d²x^k dt dl² +

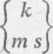
dx^m dx^s ~dt ~dt‘

Składowe kontrawariantnego wektora przyspieszenia we współrzędnych cylindrycznych wynoszą

Zadanie 5.6. Wyznaczyć dywergencję wektora kowariantnego E_k oraz laplasjan ska-lara U we współrzędnych cylindrycznych X¹ = r, x² = <p, x¹ = z, jeżeli wiadomo, że

(1)

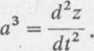
div£ = (a^mnEJ_ln

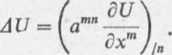
(2)

1

dt²    r dt dt

2

d²q>    2 dq dcp