str280

280 5. ZARYS RACHUNKU TENSOROWEGO

Rozwiązanie.

280 5. ZARYS RACHUNKU TENSOROWEGO

N N    N    N

Zadania do rozwiązania

1.    Uprościć wyrażenie (A_rs, + A^_r + A_srj)xśx^sx^t.

2.    Wiadomo, że T_r„ jest tensorem kowariantnym rzędu trzeciego i T_rsl + T_rts = 0 w układzie współrzędnych ,v^p. Wyznaczyć Tj_st + T'_ts w dowolnym układzie współrzędnych x'^p.

3.    Obliczyć wartości, jakie otrzymamy w przestrzeni ^-wymiarowej w wyniku następujących operacji zwężania delt Kroneckera:

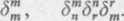
Odpowiedzi

1. 3A„_tx^rx’x^t.

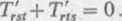
3. N, N.

§ 3. Tensory w przestrzeni Riemanna

Jak wiemy, kwadrat elementu długości luku ds² w ortogonalnym układzie współrzęd nych kartezjańskich y^k przestrzeni trójwymiarowej jest określony wzorem

(3.1)

ds² = (dy')² + (dy²)² + (dy³)².

Dla przestrzeni N-wymiarowej wzór (3.1) przybiera postać

N

(3.2)

ds² = X id/)² .

Przechodząc do dowolnych współrzędnych krzywoliniowych x^k przestrzeni Wwymia-rowej otrzymujemy po uwzględnieniu zależności (1.2) między współrzędnymi y^k i x^k oraz (1.5) we wzorze (3.2) następującą relację:

(3.3)

ds² = a_mndx^mdx",

gdzie współczynniki a_mn są funkcjami współrzędnych x*.

Ponieważ współczynniki a_mn nie występują oddzielnie, lecz jedynie w kombinacjach ^am* + ^anm’ ⁿ'^e tracimy nic na ogólności zakładając, że a_m„ są symetryczne, a więc a_mn = a„_m.

Własność 1. Zbiór Wielkości a_mn występujących we wzorze (3.3) jest symetrycznym tensorem kowariantnym rzędu drugiego.

Definicja 1. Tensorem metrycznym kowariantnym lub fundamentalnym tensorem przestrzeni nazywamy tensor a_m„ występujący w relacji (3.3).