57429 str310

310 5. ZARYS RACHUNKU TENSOROWEGO

czynnik Poissona, E — moduł Younga, a — współczynnik rozszerzalności cieplnej ciała, T — temperatura.

Rozwiązanie. W układzie ortogonalnym kartezjańskim x₂ = 'x, x₂ = y, x₃ =* z wyrażamy wzory (1), (2) i (3) w języku tensorów kartezjańskich korzystając z zależności (6.17), (6.18), (6.19), (6.21).

a) Równanie (1) przybiera postać

(1 +<r)(l — 2<r) £(l-<7)

a stąd mamy

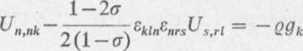
(l + ff)(l-2ff) £(1-<t)    •

b) Równanie (2) przybiera postać

(l-2ff)L^rMn+(t/_ni„)_ifc = 0,

a stąd mamy

(1—2<j) V_k„„ + U„'„_k = 0.

c) Równanie (3) przybiera postać

Zadanie 6.4. Napisać równanie przewodzenia ciepła

(1)

5T

div (k grad T) = cq —

w języku tensorów kartezjańskich dla następujących przypadków:

a)    środowisko jest jednorodne izotropowe, tzn. A = const, c = const i q = const.

b)    środowisko jest niejednorodne izotropowe, tzn. k = A(x, y, z), c = c(x, y, z) i q = Q(x,y,z).

c)    środowisko jest niejednorodne i anizotropowe, A,, = k_rs (x, y, z) jest tensorem rzędu drugiego oraz c = c()c, y, z), q = q(x, y, z).

Znaczenie symboli użytych we wzorze (1) jest następujące: T — temperatura, t — czas, k — przewodność ciepła właściwa, c — ciepło właściwe, q — gęstość środowiska.

Rozwiązanie. Dla wyrażenia równania (1) w układzie współrzędnych: x_x = x, x₂ — y, x₃ = z, ortogonalnych kartezjańskich w języku tensorów kartezjańskich korzystamy ze wzoru (6.17) i (6.18).

a) Dla środowiska jednorodnego izotropowego równanie (1) przybiera postać

k(T_n\_n = cgt,

a stąd mamy

:

A

gdzie x = —.

CQ