14856 str282

282 5. ZARYS RACHUNKU TENSOROWEGO

Definicja 7. Operacją obniżania wskaźnika nazywamy operację zwężania dokonaną

względem tegoż wskaźnika z udziałem metrycznego tensora kowariantnego, np.

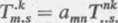
(3.10)

lub

(3.11)

Definicja 8. Operacją podwyższania wskaźnika nazywamy operację zwężania względem tegoż wskaźnika z udziałem metrycznego tensora kontrawariantnego, np.

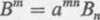
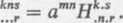
(3.12)

lub

(3.13)

Własność 8. Jeżeli w danym tensorze nastąpią dwie kolejne operacje podwyższania i obniżania względem tego samego wskaźnika, to tensor nie ulegnie zmianie.

Uwaga. Dzięki dysponowaniu metrycznym tensorem kowariantnym oraz z nim sprzężonym tensorem kontrawariantnym mogliśmy wprowadzić operacje obniżania oraz podwyższania wskaźnika.

Wprowadzenie wymienionych operacji pociąga' za sobą konieczność numerowania miejsc wskaźników w tensorach mieszanych. Dla uwidocznienia kolejnych miejsc poszczególnych wskaźników, nie zapisujemy dwóch wskaźników — jednego nad drugim, a w wolnych miejscach umieszczamy kropki, jak to zostało pokazane we wzorach (3.11) oraz (3.13).

Własność 9. Tensor metryczny iv przestrzeni Euklidesa spełnia następujący związek:

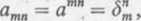
(3.14)

gdzie <5U, jest deltą Kroneckera.

Definicja 9. Długością wektora kontrawariantnego X^r nazywamy dodatnią rzeczywistą wielkość X spełniającą związek

(3.15)

gdzie e jest liczbą znakową wektora X^r (patrz wzór (3.5)).

Definicja 10. Długością wektora kowariantnego X_r nazywamy dodatnią rzeczywistą wielkość X spełniającą związek

(3.16)

v2 „ xsm \rtl

X = za XX.

Długość X nazywana jest również miarą bezwzględną wektora.

Własność 10. Jeżeli X jest długością wektora X^r (A"_r), to wektorem jednostkowym K^r (K_r) o kierunku i zwrocie wektora X’ (X_r) jest

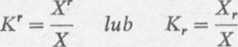
(3.17)