89710 str268 (2)

268 5. ZARYS RACHUNKU TENSOROWEGO

Definicja 7. Tensorem mieszanym rzędu M+L o M wskaźnikach kontrawariantnych i L wskaźnikach kowariantnych nazywamy zbiór wielkości    jeżeli podczas za

miany współrzędnych wielkości te transformują się zgodnie z równaniem

rpfkik2...kM

rj->P\P2...p\f

^Irir_l...r_L

dx^,k‘

dx'^k2

dx^P2

dx'^kM dx^r‘ dx^r2 dx^rL dx'^PM ' ~dx^r’¹' dć*²' ''fo*¹’

gdzie T^kl^kl;;;^k” jest tensorem w układzie współrzędnych x^r, natomiast T^‘^k2'_s'^kM jest tym samym tensorem w układzie x'^r.

W szczególnym przypadku dla M = 1 i L = 1 mamy do czynienia z tensorem mieszanym rzędu drugiego T' o jednym wskaźniku kontrawariantnym i jednym wskaźniku ko-wariantnym.

Definicja 7'. Tensorem mieszanym rzędu drugiego nazywamy zbiór wielkości T[, jeżeli podczas zamiany współrzędnych wielkości te transformują się zgodnie z równaniem

dx'^r dx^l

Należy zauważyć (patrz wzory (1.6), (1.7), (1.9), (1.10) oraz (1.11)), że górny wskaźnik jest wskaźnikiem kontrawariantnym, a dolny — kowariantnym.

(1.12)

77 = T,^k

Definicja 8. Mówimy, że dwa tensory są sobie równe, jeżeli są one tego samego typu i tego samego rzędu oraz jeżeli wszystkie składowe o tych samych wskaźnikach są sobie równe.

Definicja 9. Deltą Kroneckera nazywamy symbol określony relacją

(1.13)

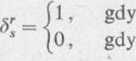
r = s, rj^s.

Własność 1. Deltę Kroneckera możemy napisać w postaci

(1.14)

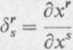
lub

(1.15)

dx* • ■ dx'^k dx^s ’

co wynika z rachunku różniczkowego, mamy bowiem

(1.16)			dx^r 3x^r 8x'^k dx^s = d7^k"dx^s'
np.
	dx^l	dx^1	dx'^1 dx^l dx'^2 8x^i dx‘
i oczywiście	d?	"a?^1*	dx^2 +dx'^2 dx^2 +dx'^2 dx

dx^l

d?

6x^l dx* dx'^N dx²

<

= 0.