63826 str300

I

300    5. ZARYS RACHUNKU TENSOROWEGO

do którego podstawiamy wartości odpowiednich składowych symbolu Christoffela rodzaju drugiego. Składowe te we współrzędnych sferycznych są przytoczone w poprzednim zadaniu (5.1). Po odpowiednich przekształceniach otrzymujemy

T_in =

d²V

Ti,2 =

Ti, 3 =

Ti,i “

T2/2 —

dg

d²V

8gdÓ~

o²V

8gd<p

d²V

dgdd

d²V

dd²

d²V

+ 0-

1 oV

~e'~80’

1 8V Q ć><P ’ 1 8V

~q' W'

dV

dg ⁷

^7:2/3 dOdcp ^Ct&°d<p’

T₃,i-

T₃,i =

d²V

cgo(p

d²V

1 8V Q 8(p ’

_n8V

d0dq> ^Clg° d(p ⁷

8²V

dV

^7,3/3=w^+QSin2d^⁺

sin 20 dV

2 J0~

Zadanie 5.3. Wyznaczyć pochodną kowariantną tensora metrycznego przestrzeni a_mn. Rozwiązanie. Dla wyznaczenia pochodnej a_mnls korzystamy z zależności (5.23), a następnie ze wzoru (4) i (4.0), mamy zatem

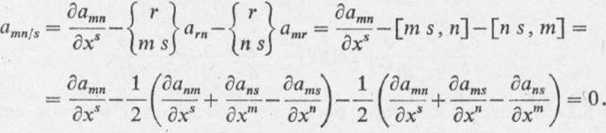
Uwzględniliśmy tutaj własność symetrii tensora metrycznego:

®mn ^rnn •

W oparciu o rozwiązanie tegoż zadania możemy sformułować następujące ogólne twierdzenie: pochodna kowariantna tensora fundamentalnego przestrzeni jest toźsamościowo równa zeru.