str 045

Dla prostszej formy wzoru na naprężenia krytyczne wprowadza się pojęcie ramienia bezwładności przekroju i . Ramię to zapisuje się w postaci wzoru

i

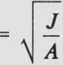
(9.16)

Wprowadza się również pojęcie smukłości pręta k, które wyraża się wzorem

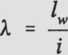
(9.17)

Dzięki temu wzór na naprężenie krytyczne przyjmie następującą prostą postać

a

kr

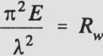
(9.18)

Naprężenia o w odniesieniu do wyboczenia nazywane są doraźną wytrzymałością na wyboczenie R_w, czyli o = R_w.

Wytrzymałość doraźna na wyboczenie zależy zatem od rodzaju materiału pręta (moduł Younga E) oraz od jego smukłości k.

Smukłość pręta zależy z kolei od długości wyboczeniowej l_w (dla pewnego jego zamocowania od długości konstrukcyjnej l) oraz od ramienia bezwładności przekroju. Z ostatniego związku wynika, że doraźna wytrzymałość na wyboczenie jest tym mniejsza, im większa jest smukłość k. Z kolei największa smukłość występuje przy najmniejszym ramieniu bezwładności, czyli

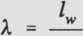
*min

(9.19)

'Anin

gdzie moment bezwładności przekroju J_min = Aź^.

Smukłość pręta zależy zatem od kierunku zginania. Dlatego należy brać pod uwagę moment bezwładności przekroju względem takiej osi przechodzącej przez środek ciężkości przekroju, przy której wartość byłaby minimalna. Wówczas określi się dla pewnych warunków mocowania pręta jego maksymalną smukłość, a następnie najmniejszą doraźną wytrzymałość na wyboczenie. Badania doświadczalne dotyczące ściskania prętów o różnych smukłoś-ciach przedstawiono na rys. 9.4 w postaci krzywej ABCD.

W zależności od smukłości pręta może wystąpić wyboczenie sprężyste (równowaga stała) lub niesprężyste (równowaga chwiejna). Przy wyboczeniu sprężystym (odcinek krzywej CD na rys. 9.4) doraźna wytrzymałość na wyboczenie R_w nie przekracza granicy proporcjonalności R_H (do której to wartości obowiązuje prawo Hook’a). Przy wyboczeniu sprężystym zatem

(9.20)

R < Rr

45